Two Circles and a Square - Problem With Solution

A problem, with a detailed solution, on a square inscribed in one circle and circumscribed around another is presented.

Problem

The square \(ABCD\) is inscribed inside the larger circle \(C_1\) and the smaller circle \(C_2\) is inscribed inside the same square. If \(A_1\) is the area of the large circle and \(A_2\) is the area of the small circle, what is the ratio \( \dfrac{A_1}{A_2} \)?

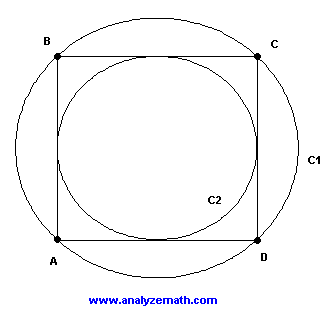
Solution to Problem

• If \( x \) is the size of one side of the square, the small circle has a diameter of size \( d = x \) and its radius is \( \frac{x}{2} \), hence its area \( A_2 \) is given by: \[ A_2 = \pi \left(\frac{x}{2}\right)^2 = \frac{\pi x^2}{4} \]
• The radius \( R \) of the large circle is equal to \( D / 2 \), where \( D \) is the diagonal of the square. By Pythagoras' theorem: \[ D^2 = x^2 + x^2 = 2x^2 \] \[ D = x \sqrt{2} \] \[ R = \frac{x \sqrt{2}}{2} \]
• The area \( A_1 \) of the large circle is given by: \[ A_1 = \pi \left(\frac{x \sqrt{2}}{2}\right)^2 = \frac{\pi x^2}{2} \]
• Hence, the ratio of the areas is: \[ \frac{A_1}{A_2} = \frac{\frac{\pi x^2}{2}}{\frac{\pi x^2}{4}} = 2 \]

More References and Links to Geometry Problems

Geometry Tutorials, Problems, and Interactive Applets.