Problems on Equilateral Triangles with Detailed Solutions
Problems on equilateral triangles are presented along with their detailed solutions.
An equilateral triangle has all three sides equal and and all three angles equal to 60° The relationship between the side \( a \) of the equilateral triangle and its area A, height h, radius R of the circumscribed and radius r of the inscribed circle are give by:
Formulas for Equilateral Triangles

Problem 1
What is the area of an equilateral triangle of perimeter 45 cm?
Problem 2
What is the area of an equilateral triangle of height 20 units?
Problem 3
What is the area of the circumscribed circle of an equilateral triangle of side a = 5 inches?
Problem 4
What is the radius of the inscribed circle of an equilateral triangle with an area of 100 cm 2?
Problem 5
What is the ratio of the area of the circumscribed circle to the area of the inscribed circle of an equilateral triangle?
Problem 6
What is the area of triangle CA'B' if ABC is an equilateral triangle and A'B' is parallel to AB?

Problem 7
What is is the area of the shaded (in green) shape shown below if ABC is an equilateral triangle of side a = 10 has an inscribed circle, with center O, and is tangent at P and M to the sides AC and AB respectively?

Problem 8
Find the coordinates of point C such that triangle ABC is equilateral of side 12 units.
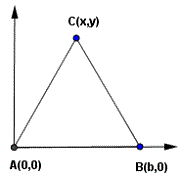
Problem 9
What is the area of the triangle BB'B" if ABC is an equilateral triangle of side 10 units and A'B' is parallel to AB?

Problem 10
What is the area of the shaded shape (in red) if all three circles have equal radii of 15 units and are tangent to each other?

Solutions to the Above Questions
-
Solution
If the side of the equilateral triangle is \( a \), its perimeter P is given by
P = 3 \( a \)
\( a \) = P / 3 = 45 / 3 = 15 cm
Area A = \( a^2\dfrac{\sqrt 3}{4} \) = = \( 15^2\dfrac{\sqrt 3}{4} \) = \( \dfrac{225} {4} {\sqrt 3} \) cm 2
-
Solution
If h is the height of the equilateral triangle and \( a \) its side, we have the relationship (see formula above)
h = \( a \dfrac{\sqrt 3}{2} \)
h = 20, hence the equation: 20 = \( a\dfrac{\sqrt 3}{2} \)
Solve for \( a \) to get : \( a = \dfrac{40}{\sqrt 3} \)
Area A = \( a^2\dfrac{\sqrt 3}{4} \) = = \( (\dfrac{40}{\sqrt 3})^2\dfrac{\sqrt 3}{4} = \dfrac{400}{3} \sqrt 3 \) unit 2
-
Solution
Let R be the radius the circumscribed circle to an equilateral triangle of side a, then (see formula above)
R = \( a\dfrac{\sqrt 3}{3} \) = \( 5 \dfrac{\sqrt 3}{3} \) , \( a = 5\) given
Area of circle of radius R = \( \pi R^2 = \pi (5\dfrac{\sqrt 3}{3})^2 = \dfrac{25}{3}\pi \) inches 2
-
Solution
Let r be the radius the inscribed circle to an equilateral triangle of side a, then (see formula above)
r = \( a\dfrac{\sqrt 3}{6} \)
Square both sides of the above to get : r 2 = \( \dfrac{a^2}{12} \)
Area A of circle of radius r is given by: A = \( \pi r^2 = \pi \dfrac{a^2}{12} \)
The area of the equilateral triangle is given, hence: 100 = \( a^2\dfrac{\sqrt 3}{4} \)
Solve the above to find: \( a^2 = \dfrac{400} {\sqrt 3}\)
Substitute a 2 found above into the expression of the area A = \( = \pi \dfrac{a^2}{12} \) found above to find
A = \( = \pi \dfrac{\dfrac{400} {\sqrt 3}}{12} = \pi \dfrac{100\sqrt 3}{9} \) cm 2
-
Solution
If R is the radius of the circumscribed circle and r the radius the inscribed circle to an equilateral triangle of side a, then the ratio S is given by
\( S = \dfrac{\pi R^2}{\pi r^2} = \dfrac{ R^2} {r^2} = (\dfrac{ R} {r})^2 \)
We now use the formulas for R and r given above and simplify
\( S = \left(\dfrac{ a\dfrac{\sqrt 3}{3} } {a\dfrac{\sqrt 3}{6}} \right)^2 = 4\)
-
Solution
Since A'B' is parallel to AB, triangles ABC and AB'C' are similar and therefore triangle AB'C' is also equilateral and has side equal to 4.
Area of AB'C' = \( 4^2\dfrac{\sqrt 3}{4} = 4 \sqrt 3 \) unit 2
-
Solution
Area of green shape = area of quadrilateral AMOP - area of sector MOP
Quadrilateral AMOP is made up of two congruent right triangles (AC perpendicular to PO and AB perpendicular to MO) since P and M are points of tangency. (Note: AP = a/2)
area of triangle APO = (1/2) AP × PO = (1/2) AP × r = (1/2) (10 / 2) × \( 10 \dfrac{\sqrt 3}{6} = \dfrac{25\sqrt 3}{6}\)
Angle of sector MOP = 360 / 3 = 120°
area of sector MOP = (1/2) (120 π / 180 ) r 2 = \( \dfrac{\pi}{3} (10\dfrac{\sqrt 3}{6})^2 = 50\pi / 18 \)
Area of green shape = 2 × area of triangle APO - area of sector MOP = \( \dfrac{50\sqrt 3}{6} - 50\pi / 18 \)
-
Solution
AB = \( \sqrt{b^2} \) = 12
Solve for b
b = 12
AC = \( \sqrt{(x^2 +y^2)} \) = 12 gives \( x^2 +y^2 = 12^2\)
BC = \( \sqrt{((x-12)^2 +y^2)} \) = 12 gives \( (x-12)^2 +y^2 = 12^2 \)
Expand the last equation: \( x^2 -24x + 12^2 + y^2 = 12^2 \)
Use \( x^2 +y^2 = 12^2\) in the last equation to obtain
\( 24 x = 12^2 \) , solve for x: x = 6
Substitute x = 6 in the equation \( x^2 +y^2 = 12^2 \) to find y = 6 √3
-
Solution
Since A'B' is parallel to AB, triangles ABC and AB'C' are similar and both equilateral. Hence CB' = 4 and B'B = 10 - 4 = 6
Angle BB'B'' has a size of 30° since the size of angle B'BB" is 60°.
sin(30°) = BB" / BB' , hence BB" = 3 and use Pythagora's to get B'B" = 3√3
area of triangle BB'B" = (1/2) B'B" × BB" = (1/2) 3√3 × 3 = 4.5√3 unit 2
-
Solution

Figure above shows that the centers of the circles make an equilateral triangle of side 2r where r = 15 (given) is the radius of one circle.
The area of the red shape = area of the equilateral triangle - areas of three congruent sectors (each sector has 60° angle)
area of the equilateral triangle = \( (2r)^2\dfrac{\sqrt 3}{4} = 30^2\dfrac{\sqrt 3}{4} \)
areas of three congruent sectors = 3 × area of one sector = 3 × (1/2) ( 60 π /180) r 2 = 15 2 π /2
The area of the red shape = \( ( 30^2\dfrac{\sqrt 3}{4} - 15^2 \dfrac{\pi}{2} ) \) unit 2
More References and Links to Geometry Problems
Geometry Tutorials, Problems and Interactive Applets.







