
The intersecting secant tangent theorem [1] states that for the secant \( A B \) and tangent \( O T \), there is relationship between the lengths of the segments as follows: \[ OT^2 = OA \times OB \]
Consider the circle , the secants \( A B \) and the tangent \( OT\) in the figure below.

The intersecting secant tangent theorem [1] states that for the secant \( A B \) and tangent \( O T \), there is relationship between the lengths of the segments as follows: \[ OT^2 = OA \times OB \]
Note that none of the figures below is drawn to scales.
Question 1
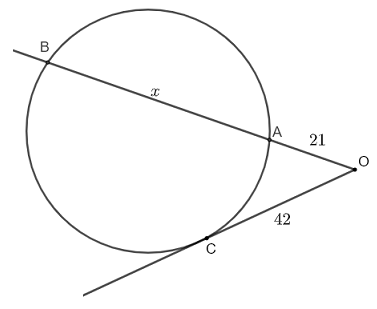
In the figure below, \( OC \) is tangent to the circle. Find \( x = AB\), given the lengths of segments \( OC = 42 \) and \( OA = 21\) .
Solution
Apply the intersecting secant tangent theorem above to the secant \( OB \) and tangent \( OC \) to write: \( \quad OC^2 = OA \times OB \)
Substitute the known and given quantities: \( \quad 42^2 = 21 \times (21 + x) \)
Expand and simplify: \( \quad 1323 = 21 x \)
Solve for \( x \): \( \quad x = 63\)
Question 2
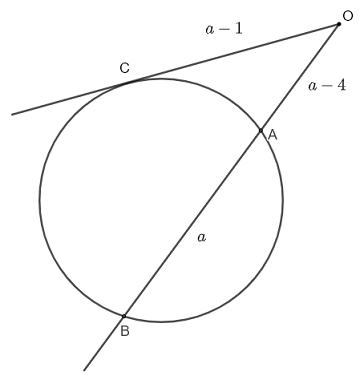
In the figure below, \( OC \) is tangent to the circle. Find \( a \) given the lengths of segments \( OC = a - 1 , OA = a - 4, AB = a \).
Solution
\( OB \) is secant and \( OC \) is tangent hence the intersecting secant tangent theorem gives: \( \quad OC^2 = OA \times OB \)
Substitute the given quantities: \( \quad (a-1)^2 = (a-4)(a-4+a) \)
Expand and group like terms: \( \quad a^2 - 2 a + 1 = 2a^2-12a+16 \)
Rewrite the above quadratic equation in standard form as follows: \( a^2-10a+15 = 0 \)
Solve for \( a \) to obtain two solutions: \( a=5 + \sqrt{10} \) and \( a = 5 - \sqrt{10} \)
Note The length of a segment must be positive. Hence \( a = 5 - \sqrt{10} \) cannot be accepted as a solution because \( OA = a - 4 = 5 - \sqrt{10} - 4 = 1-\sqrt{10} \) is negative
\( a = 5 + \sqrt{10} \) is the only solution to the given question.
Question 3
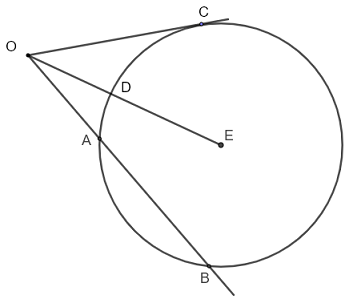
In the figure below, \( OC \) is tangent to the circle and \( OE \) intersects the circle at point \( D \) where \( E \) is the center of the circle. The lengths of the segments \( OC \) and \( OD \) are given by \( OD = 6 \) and \( OC = r + 3 \) where \( r \) is the length of the radius of the circle.
1) Find \( r \)
2) Find the lengths of the segments \( OA \) and \( AB \) such that \( AB = 2 OA \)
Solution
1) Since \( OC \) is tangent to the circle and \( E \) is the center, then \( EC \) is a radius and is perpendicular to \( OC \).
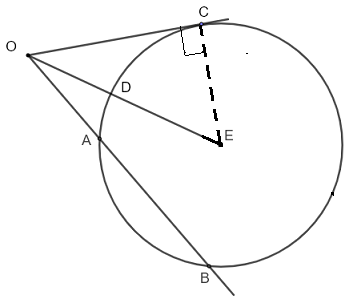
Use the Pythagorean theorem to write: \( \quad (OD + DE)^2 = EC^2 + OC^2 \)
Note that \( DE \) is a radius and substitute by the given quantities: \( \quad (6+r)^2 = r^2 + (r+3)^2 \)
Expand and write the above equation in standard form: \( \quad -r^2+6r+27 = 0 \)
Solve for \( r \) to obtain two solutions: \( r = -3 \) and \( r = 9 \) and only the solution \( r = 9 \) is valid since the length of the radius is a positive quantity.
2) The use of the intersecting secant tangent theorem gives: \( \quad OC^2 = OA \times OB \)
Substitute the known and unknown quantities: \( \quad (9 + 3)^2 = OA \times (O A + 2 O A) \)
The above may be written as \( \quad (15)^2 = 3 OA^2 \)
Solve for \( OA \): \( \quad OA = \dfrac{15}{\sqrt 3} \) , \( AB = 2 \dfrac{15}{\sqrt 3} \)