Problems on Isosceles Triangles with Detailed Solutions

Ten challenging problems on isosceles triangles with comprehensive step-by-step solutions.

Isosceles Triangle Formulas

An isosceles triangle has two equal sides with the angles opposite them equal. The relationships between:

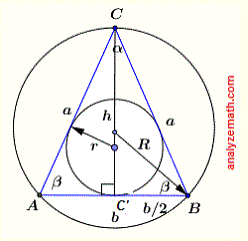
Isosceles triangle diagram

are given by:

\[ A = \frac{1}{2} b h \] \[ h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} \] \[ r = \frac{b}{2} \sqrt{\frac{2a-b}{2a+b}} \] \[ R = \frac{a^2}{\sqrt{4a^2 - b^2}} \]

Practice Problems

Problem 1

Find the area of an isosceles triangle with base \( b = 8 \, \text{cm} \) and lateral side \( a = 5 \, \text{cm} \).

Problem 2

Find the base of an isosceles triangle with lateral side \( a = 5 \, \text{cm} \) and area \( A = 6 \, \text{cm}^2 \).

Problem 3

Find the lateral side of an isosceles triangle with area \( A = 20 \, \text{units}^2 \) and base \( b = 10 \, \text{units} \).

Problem 4

Find the lateral side of an isosceles triangle where the height \( h \) is 4 cm shorter than the base \( b \), and the area is \( 30 \, \text{cm}^2 \).

Problem 5

\( \triangle ABC \) and \( \triangle BCD \) are isosceles triangles. Find \( \angle BDE \).

Two isosceles triangles

Problem 6

\( \triangle ABC \) and \( \triangle CDE \) are isosceles triangles. Find \( \angle CED \).

Two isosceles triangles

Problem 7

Find the area of the circle inscribed in an isosceles triangle with base \( b = 10 \) and lateral side \( a = 12 \).

Problem 8

Find the ratio \( R/r \) for an isosceles triangle with \( a = 2b \).

Problem 9

Find the lateral side and base of an isosceles triangle with height \( h = 16 \, \text{cm} \) and circumradius \( R = 9 \, \text{cm} \).

Problem 10

Find the area of an isosceles triangle with lateral side \( 2 \) that is similar to another isosceles triangle with lateral side \( 10 \) and base \( 12 \).

Solutions

  1. Solution:
    Using Pythagorean theorem: \( h = \sqrt{a^2 - (b/2)^2} = \sqrt{5^2 - 4^2} = 3 \, \text{cm} \)
    Area: \( A = \frac{1}{2} b h = \frac{1}{2} \times 8 \times 3 = 12 \, \text{cm}^2 \)
  2. Solution:
    Using area formula: \( A = \frac{1}{2} a^2 \sin\alpha \Rightarrow \sin\alpha = \frac{2A}{a^2} = \frac{12}{25} \)
    \( \alpha = \arcsin(12/25) \)
    From geometry: \( \sin(\alpha/2) = \frac{b/2}{a} = \frac{b}{2a} \)
    \( b = 2a \sin(\alpha/2) = 10 \sin\left(\frac{1}{2} \arcsin\frac{12}{25}\right) \approx 2.48 \, \text{cm} \)
  3. Solution:
    From area: \( A = \frac{1}{2} b h \Rightarrow 20 = \frac{1}{2} \times 10 \times h \Rightarrow h = 4 \)
    Lateral side: \( a = \sqrt{(b/2)^2 + h^2} = \sqrt{5^2 + 4^2} = \sqrt{41} \)
  4. Solution:
    Given \( h = b - 4 \) and \( A = \frac{1}{2} b h = 30 \)
    \( \frac{1}{2} b (b - 4) = 30 \Rightarrow b^2 - 4b - 60 = 0 \)
    Positive solution: \( b = 10 \, \text{cm}, \, h = 6 \, \text{cm} \)
    Lateral side: \( a = \sqrt{(b/2)^2 + h^2} = \sqrt{25 + 36} = \sqrt{61} \, \text{cm} \)
  5. Solution:
    In \( \triangle ABC \): \( \angle CAB = \angle CBA = \frac{180^\circ - 66^\circ}{2} = 57^\circ \)
    In \( \triangle BCD \): \( \angle CBD = \angle CDB = 45^\circ \)
    Angles on straight line: \( \angle DBE = 180^\circ - 57^\circ - 45^\circ = 78^\circ \)
    In \( \triangle BDE \): \( \angle BDE = 90^\circ - 78^\circ = 12^\circ \)
  6. Solution:
    \( \angle ABC = 180^\circ - 116^\circ = 64^\circ \)
    In \( \triangle ABC \): \( \angle BCA = 180^\circ - 2 \times 64^\circ = 52^\circ \)
    \( \angle DCE = \angle BCA = 52^\circ \) (vertical angles)
    In \( \triangle CDE \): \( \angle CED = 180^\circ - 2 \times 52^\circ = 76^\circ \)
  7. Solution:
    Inradius: \( r = \frac{b}{2} \sqrt{\frac{2a-b}{2a+b}} = 5 \sqrt{\frac{4}{34}} = 5\sqrt{\frac{2}{17}} \)
    Circle area: \( A = \pi r^2 = \pi \left(5\sqrt{\frac{2}{17}}\right)^2 = \frac{50\pi}{17} \)
  8. Solution:
    Circumradius: \( R = \frac{a^2}{\sqrt{4a^2 - b^2}} = \frac{(2b)^2}{\sqrt{4(2b)^2 - b^2}} = \frac{4b}{\sqrt{15}} \)
    Inradius: \( r = \frac{b}{2} \sqrt{\frac{2a-b}{2a+b}} = \frac{b}{2} \sqrt{\frac{3}{5}} \)
    Ratio: \( \frac{R}{r} = \frac{4b/\sqrt{15}}{(b/2)\sqrt{3/5}} = \frac{8}{\sqrt{9}} = \frac{8}{3} \)
  9. Solution:
    From Pythagorean theorem: \( 4a^2 - b^2 = 4h^2 \)
    Circumradius formula: \( R = \frac{a^2}{\sqrt{4a^2 - b^2}} = \frac{a^2}{2h} \)
    \( 9 = \frac{a^2}{32} \Rightarrow a^2 = 288 \Rightarrow a = 12\sqrt{2} \, \text{cm} \)
    \( b = \sqrt{4a^2 - 4h^2} = \sqrt{4 \times 288 - 4 \times 256} = \sqrt{128} = 8\sqrt{2} \, \text{cm} \)
  10. Solution:
    For larger triangle: \( h = \sqrt{10^2 - 6^2} = 8 \)
    Area: \( A_2 = \frac{1}{2} \times 12 \times 8 = 48 \)
    Ratio of similarity: \( k = \frac{2}{10} = \frac{1}{5} \)
    Area ratio: \( k^2 = \frac{1}{25} \)
    Smaller triangle area: \( A_1 = 48 \times \frac{1}{25} = 1.92 \, \text{units}^2 \)

Additional Resources

Geometry Tutorials, Problems and Interactive Applets

Home Page