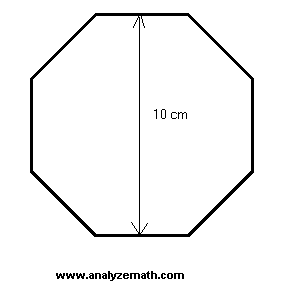
Given a regular octagon with distance \(10\) cm between two opposite sides (span), find:

A regular octagon has \(8\) sides. The measure of one interior angle is: \[ \frac{(8-2) \times 180^\circ}{8} = 135^\circ \]

Consider triangle \(ABC\) where \(AC \perp BC\). Since the interior angle is \(135^\circ\), angle \(ABC\) is: \[ 135^\circ - 90^\circ = 45^\circ \] Thus, triangle \(ABC\) is an isosceles right triangle.
Let \(x\) be the side length of the octagon and \(y\) be the equal legs of triangle \(ABC\). The span of \(10\) cm equals \(x + 2y\): \[ x + 2y = 10 \quad \text{(1)} \] By the Pythagorean theorem in triangle \(ABC\): \[ x^2 = y^2 + y^2 = 2y^2 \quad \text{(2)} \]
From equation (2): \( y = \frac{x}{\sqrt{2}} \).
Substitute into equation (1):
\[
x + 2\left(\frac{x}{\sqrt{2}}\right) = 10
\]
\[
x + \sqrt{2}x = 10
\]
\[
x(1 + \sqrt{2}) = 10
\]
\[
x = \frac{10}{1 + \sqrt{2}} \ \text{cm}
\]
Rationalizing the denominator:
\[
x = \frac{10}{1 + \sqrt{2}} \cdot \frac{1 - \sqrt{2}}{1 - \sqrt{2}} = 10(\sqrt{2} - 1) \ \text{cm}
\]
Numerically: \( x \approx 4.142 \ \text{cm} \)
\[ P = 8x = 8 \times \frac{10}{1 + \sqrt{2}} = \frac{80}{1 + \sqrt{2}} \ \text{cm} \] Rationalized form: \[ P = 80(\sqrt{2} - 1) \ \text{cm} \quad (\approx 33.137 \ \text{cm}) \]
Method: Subtract areas of four right triangles from the area of the bounding square of side \(10\) cm. \[ A = 10^2 - 4 \times \left( \frac{1}{2} y^2 \right) = 100 - 2y^2 \] From equation (2): \( y^2 = \frac{x^2}{2} \). Thus: \[ A = 100 - 2 \left( \frac{x^2}{2} \right) = 100 - x^2 \] Substitute \( x = 10(\sqrt{2} - 1) \): \[ x^2 = 100(3 - 2\sqrt{2}) \] \[ A = 100 - 100(3 - 2\sqrt{2}) = 100(1 - 3 + 2\sqrt{2}) = 200(\sqrt{2} - 1) \ \text{cm}^2 \] Numerically: \( A \approx 82.842 \ \text{cm}^2 \)