Parallelogram Geometry Problems

Detailed parallelogram problems with step-by-step solutions covering area, angles, side lengths, and coordinate geometry.

Parallelogram Formulas

• Area: \( A = b \times h \) where \( b \) is base and \( h \) is altitude
• Opposite sides: Parallel and equal in length
• Opposite angles: Equal in measure
• Consecutive angles: Supplementary (sum to \( 180^\circ \))

Problem 1: Coordinate Geometry Verification

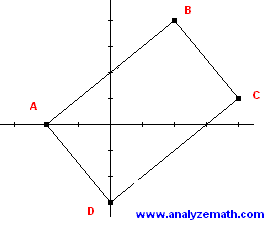
Prove that quadrilateral ABCD with vertices \( A(-2, 0) \), \( B(2, 4) \), \( C(4, 1) \), and \( D(0, -3) \) is a parallelogram.

Problem 2: Side Length and Height Calculation

Given side \( AB = 15 \) ft, angle \( D = 135^\circ \), and area \( = 1000 \) ft², find height \( h \) and side \( BC \).

Problem 3: Angle Bisector Geometry

In parallelogram ABCD, BB' bisects angle B and CC' bisects angle C. Given \( BC = 10 \) m, find lengths \( x \) and \( y \).

Problem 4: Internal Angles from Area

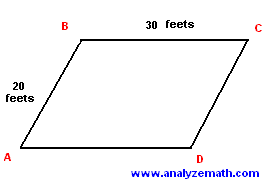
Find all internal angles of a parallelogram with sides 20 ft and 30 ft and area 300 ft².

Detailed Solutions

Solution to Problem 1

Approach: Verify two pairs of parallel and congruent sides.

Slope calculations:

• Slope \( AB = \frac{4 - 0}{2 - (-2)} = 1 \)
• Slope \( BC = \frac{1 - 4}{4 - 2} = -\frac{3}{2} \)
• Slope \( CD = \frac{-3 - 1}{0 - 4} = 1 \)
• Slope \( DA = \frac{-3 - 0}{0 - (-2)} = -\frac{3}{2} \)

Distance calculations:

• \( AB = \sqrt{(4)^2 + (4)^2} = 4\sqrt{2} \)
• \( BC = \sqrt{(2)^2 + (-3)^2} = \sqrt{13} \)
• \( CD = \sqrt{(4)^2 + (4)^2} = 4\sqrt{2} \)
• \( DA = \sqrt{(-2)^2 + (3)^2} = \sqrt{13} \)

Conclusion: \( AB \parallel CD \) (equal slopes) and \( AB = CD \). \( BC \parallel DA \) (equal slopes) and \( BC = DA \). Thus, ABCD is a parallelogram.

Solution to Problem 2

Step 1: Find angle A

Consecutive angles are supplementary: \( \angle A = 180^\circ - 135^\circ = 45^\circ \)

Step 2: Calculate height h

Using right triangle ABB': \( \sin 45^\circ = \frac{h}{15} \)

\( h = 15 \times \frac{\sqrt{2}}{2} = \frac{15\sqrt{2}}{2} \) ft

Step 3: Find side BC

Area formula: \( A = BC \times h \)

\( 1000 = BC \times \frac{15\sqrt{2}}{2} \)

\( BC = \frac{1000 \times 2}{15\sqrt{2}} = \frac{2000}{15\sqrt{2}} \approx 94.28 \) ft (rounded)

Solution to Problem 3

Step 1: Analyze angles

In triangle BOC: \( \angle BCO = \frac{1}{2}\angle C \), \( \angle CBO = \frac{1}{2}\angle B \)

Since \( \angle B + \angle C = 180^\circ \), then \( \angle BCO + \angle CBO = 90^\circ \)

Thus \( \angle BOC = 90^\circ \) (triangle angle sum).

Step 2: Find angle BCO

In parallelogram, \( \angle C = \angle A = 60^\circ \) (from diagram)

\( \angle BCO = \frac{60^\circ}{2} = 30^\circ \)

Step 3: Calculate x and y

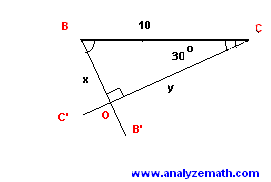
In right triangle BOC:

• \( \sin 30^\circ = \frac{x}{10} \Rightarrow x = 10 \times \frac{1}{2} = 5 \) m
• \( \cos 30^\circ = \frac{y}{10} \Rightarrow y = 10 \times \frac{\sqrt{3}}{2} = 5\sqrt{3} \approx 8.66 \) m

Solution to Problem 4

Step 1: Area relationship

Area of parallelogram = \( 2 \times \) area of triangle ABC

Area of triangle ABC = \( \frac{1}{2} \times 30 \times 20 \times \sin(\angle B) \)

Thus: \( 300 = 2 \times \frac{1}{2} \times 30 \times 20 \times \sin(\angle B) \)

Step 2: Solve for angle B

\( 300 = 600 \times \sin(\angle B) \)

\( \sin(\angle B) = 0.5 \)

\( \angle B = 150^\circ \) (since \( \sin 30^\circ = \sin 150^\circ = 0.5 \), and angle B > 90° in parallelogram)

Step 3: Find all angles

• \( \angle B = 150^\circ \)
• \( \angle D = \angle B = 150^\circ \) (opposite angles equal)
• \( \angle A = 180^\circ - 150^\circ = 30^\circ \) (consecutive angles supplementary)
• \( \angle C = \angle A = 30^\circ \)

More Geometry Resources: Geometry Tutorials and Interactive Problems