The definition and properties of the perpendicular bisector are presented along with problems and their detailed solutions.
Note that the figures below are not drawn to scale and therefore the problems below are not to be solved using the sizes of angles, segments, ... in the figures.

Definition of Perpendicular Bisector

The perpendicular bisector of a line segment AB is a line that is perpendicular to AB and passes through the midpoint of segment AB.(see figure below).
\( \overline{MA} = \overline{MB} \) To construct a perpendicular bisector of segment \( AB\), we may proceed as follows:
1 - draw two circles centered at A and B and with equal radii larger than half the length of segment \( AB \).
2 - connect the intersections P and Q of the two circles to make a line. This line is perpendicular to AB and passes through the midpoint M of segment AB.(see figure below).

Perpendicular Bisector of a Triangle and Cicumcenter

Problems with Solutions

Problem 1
In the figure below, \( DE \) is the perpendicular bisector to segment \( AB \) whose length is equal to \( 4 \) units.
a) Find the size of angle \( x \).
b) Find the area of triangle \( ABC \).


Solution to Problem 1
a)
Since \( DE \) is the perpendicular bisector to segment \( AB \), \( DE \) and \( AB \) are perpendicular and therefore \( \angle CFA = 90^{\circ} \) and the sum of all angles of triangle \( AFC \) is equal to \( 180^{\circ} \)

\( 36^{\circ} + \angle ACF + 90^{\circ} = 180^{\circ} \)
Solve for \( \angle ACF \) to obtain
\( \angle ACF = 54^{\circ} \)
Angles \( \angle ACF \) and \( x \) are vertical angles and therefore congruent; hence \( x = 54^{\circ} \)

b)
\( FC \) is the height of triangle \( ABC \) and its length is given by
\( \overline{FC} = \overline{FA} \tan(36^{\circ}) \)
Since \(DE \) is a perpendicular bisector, \( \overline{AB} = 4 \) and \( \overline{FA} \) is given by
\( \overline{FA} = \dfrac{1}{2} \overline{AB} = 2 \)
The area \( A \) of triangle \( ABC \) is given
\( A = \dfrac{1}{2} \times base \times height \)
Substitute
\( A = \dfrac{1}{2} \times \overline{AB} \times \overline{FC} \)
Substitute by numerical values
\( A = \dfrac{1}{2} \overline{AB} \times 2 \times \tan(36^{\circ}) \approx 2.9\) square units

Problem 2
In the figure below, \( DM \) is the perpendicular bisector to segment \( AB \) whose length is equal to \( 4 \) units and \( DN \) is the perpendicular bisector to segment \( BC \) whose length is equal to \( 6 \) units.
Find the area of the quadrilateral \( MDNB \) if the length of segment \( BD \) is equal to \( 7 \) units.


Solution to Problem 2
The quadrilateral \( MDNB \) is not any of the quadrilateral whose formula of the area is known, we therefore need to split it into figures whose area may be calculated. It is here suggested to calculate the area of the quadrilateral \( MDNB \) as the sum of the areas of triangles \( BDM \) and \( BDN \). (see figure below)
Since \( DM \) is a perpendicular bisector for segment \( AB \), we conclude that
\( \overline{MB} = \dfrac{1}{2} \overline{AB} = 2 \)
and \( BDM \) is a right triangle. (see figure below)
Using the Pythagorean theorem , we can write
\( \overline{BD}^2 = \overline{MB}^2 + \overline{MD}^2 \)
Substitute the known quantities
\( 7^2 = 2^2 + \overline{MD}^2 \)
Solve for \( \overline{MD} \)
\( \overline{MD} = \sqrt{45} = 3 \sqrt 5\)

Since \( DN \) is a perpendicular bisector for segment \( BC \), we conclude that
\( \overline{NB} = \dfrac{1}{2} \overline{BC} = 3 \)
and \( BDN \) is a right triangle.
Use the Pythagorean theorem to write
\( \overline{BD}^2 = \overline{NB}^2 + \overline{ND}^2 \)
Substitute the known quantities
\( 7^2 = 3^2 + \overline{MD}^2 \)
Solve for \( \overline{ND} \)
\( \overline{ND} = \sqrt{40} = 2 \sqrt {10}\)

Area of triangle \( BDM = \dfrac{1}{2} \overline{MB} \overline{MD} = \dfrac{1}{2} \times 2 \times 3 \sqrt 5 = 3 \sqrt 5 \)
Area of triangle \( BDN = \dfrac{1}{2} \overline{NB} \overline{ND} = \dfrac{1}{2} \times 3 \times 2 \sqrt {10} = 3 \sqrt {10} \)
The area \( A \) of the quadrilateral \( MDNB \) as the sum of the areas of triangles \( BDM \) and \( BDN \), hence
\( A = 3 \sqrt 5 + 3 \sqrt {10} = 3 (\sqrt 5 + \sqrt {10}) \approx 16.2 \) square units.

Problem 3
In the figure below, \( AD \) is parallel to \( BC \) and \( FE \) is the perpendicular bisector to segment \( AD \) whose length is equal to half the length of segment \( BC \).
Find the ratio of the area of triangle \( AEF\) given that the area of the trapezoid \( ABCD\) is 120 square units.


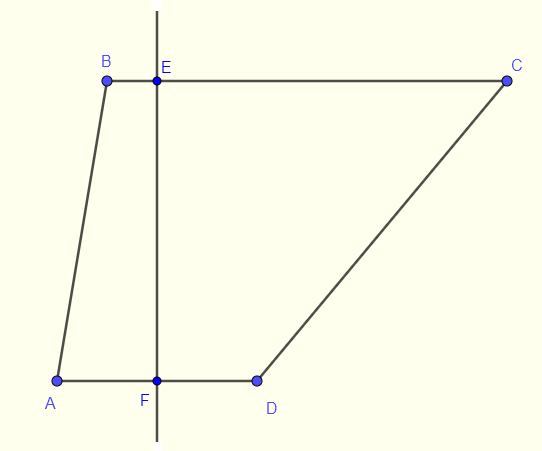
Solution to Problem 3

Since \( FE \) is a perpendicular bisector for segment \( AD \), we conclude that
\( \overline{AF} = \dfrac{1}{2} \overline{AD}\)
and
\( AEF \) is a right triangle. (see figure below)
The area \( A_1 \) of triangle \( AEF \) is given by
\( A_1 = \dfrac{1}{2} \times \overline{AF} \times \overline{EF} \)
The area \( A_2 \) of the trapezoid \( ABCD \) is given by
\( A_2 = \dfrac{1}{2} \times (\overline{BC} + \overline{AD} ) \times \overline{EF} \)
The ratio \( \dfrac{A_2}{A_1} \) is given by
\( \dfrac{A_2}{A_1} = \dfrac{\dfrac{1}{2} \times (\overline{BC} + \overline{AD} ) \times \overline{EF}}{\dfrac{1}{2} \times \overline{AF} \times \overline{EF}} \)


Simplify
\( \dfrac{A_2}{A_1} = \dfrac{\overline{BC} + \overline{AD} }{\overline{AF} } \)
We are also given that
\( \overline{AD} = \dfrac{1}{2} \overline{BC} \)
Hence
\( \overline{AF} = \dfrac{1}{2} \overline{AD} = \dfrac{1}{4} \overline{BC}\)
Substitute
\( \dfrac{A_2}{A_1} = \dfrac{\overline{BC} + \dfrac{1}{2} \overline{BC} }{\dfrac{1}{4} \overline{BC}} \)
Simplify
\( \dfrac{A_2}{A_1} = \dfrac{ 1 + \dfrac{1}{2} }{\dfrac{1}{4}} = 6 \)
Hence
\( A_1 = \dfrac{A_2}{6} = \dfrac{120}{6} = 20 \) square units

More References and Links to Geometry Problems