Polygon Problems with Solutions

Question: A regular hexagon is inscribed in a circle of radius 10 cm. Find the length of one side of the hexagon.

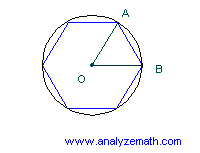
Solution:

• Angle \(\angle AOB = \frac{360^\circ}{6} = 60^\circ\)
• Since \(OA = OB = 10\) cm, triangle \(OAB\) is isosceles.
• Since \(\triangle OAB\) has equal angles, it is equilateral, so \(AB = 10\) cm.

Question: A regular pentagon is circumscribed around a circle of radius 6 cm. Find the length of one side of the pentagon (approximate to two decimal places).

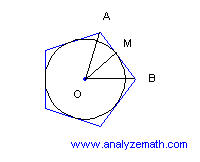
Solution:

• Let \(t\) be the size of angle \(AOB\), hence: \(t = \frac{360^\circ}{5} = 72^\circ\)
• Triangle \(MOB\) is a right triangle; using trigonometry: \(\tan\left(\frac{t}{2}\right) = \frac{MB}{OM}\)
• \(MB = OM \tan\left(\frac{t}{2}\right) = 6 \tan(36^\circ)\)
• Side of pentagon \(= 2 \times MB = 2 \times 6 \times \tan(36^\circ) \approx 8.7\) cm.

Question: Find the area of a dodecagon with side length 6 mm (approximate to one decimal place).

Solution:

• A dodecagon is a regular polygon with 12 sides and the central angle \(t\) opposite one side of the polygon is given by:
• \(t = \frac{360^\circ}{12} = 30^\circ\)
• Using the formula: \(A = \frac{1}{4} n s^2 \cot\left(\frac{180^\circ}{n}\right)\)
• Substituting \(n = 12, s = 6\), we get \(A \approx 403.1\) mm\({}^2\).

Question: Show that as the number of sides \(n\) of a polygon inscribed in a circle of radius \(R\) increases, the area of the polygon approaches the area of the circle.

Solution:

• We now use the formula for the area when the side of the regular polygon is known.
• Area of the polygon: \(A_n = \frac{1}{2} n R^2 \sin\left(\frac{2\pi}{n}\right)\)
• For large \(n\), \(\sin\left(\frac{2\pi}{n}\right) \approx \frac{2\pi}{n}\), so \(A_n \approx \pi R^2\), which is the area of the circle.