Trapezoid Geometry Problems
Practice solving trapezoid problems involving area, height, and side lengths with detailed solutions.
Trapezoid Area Formula
The area of a trapezoid is given by:
\[ A = \frac{1}{2} h (a + b) \]
where \( h \) is the height (altitude) and \( a \), \( b \) are the lengths of the parallel bases.
Problems
Problem 1
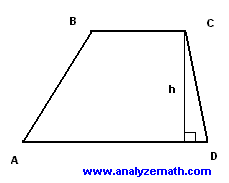
Trapezoid \( ABCD \) has \( AD \parallel BC \), \( \angle D = 40^\circ \), \( DC = 2 \text{ m} \), \( BC = 5 \text{ m} \), and area \( = 20 \text{ m}^2 \). Find the length of \( AD \).
Problem 2
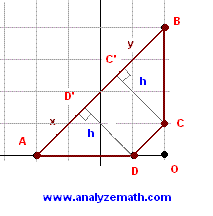
Show that quadrilateral \( ABCD \) with vertices \( A(-2,0) \), \( B(2,4) \), \( C(2,1) \), and \( D(1,0) \) is a trapezoid and calculate its area.
Problem 3
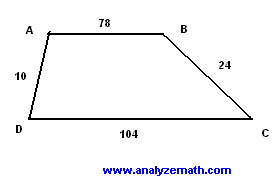
Find the area of trapezoid \( ABCD \) given its side lengths: \( AB = 78 \), \( BC = 24 \), \( CD = 104 \), \( DA = 10 \), with \( AB \parallel CD \).
Solutions
Solution to Problem 1
- Find height \( h \) using right triangle trigonometry:
\[ \sin 40^\circ = \frac{h}{DC} \Rightarrow h = 2 \sin 40^\circ \]
- Substitute into area formula:
\[ 20 = \frac{1}{2} \cdot 2 \sin 40^\circ \cdot (5 + AD) \]
- Solve for \( AD \):
\[ 20 = \sin 40^\circ (5 + AD) \Rightarrow AD = \frac{20}{\sin 40^\circ} - 5 \approx 26.11 \text{ m} \]
Solution to Problem 2
- Calculate slopes to check parallelism:
\[ \text{slope of } AB = \frac{4-0}{2-(-2)} = 1, \quad \text{slope of } BC = \frac{1-4}{2-2} \text{ (undefined)} \]
\[ \text{slope of } CD = \frac{0-1}{1-2} = 1, \quad \text{slope of } DA = \frac{0-0}{-2-1} = 0 \]
Since \( AB \) and \( CD \) have equal slopes, \( AB \parallel CD \), confirming a trapezoid.
- Calculate area by subtracting triangle areas:
\[ \text{Area of } \triangle ODC = \frac{1}{2} \times 1 \times 1 = 0.5 \]
\[ \text{Area of } \triangle OAB = \frac{1}{2} \times 4 \times 4 = 8 \]
\[ \text{Area of trapezoid } ABCD = 8 - 0.5 = 7.5 \text{ units}^2 \]
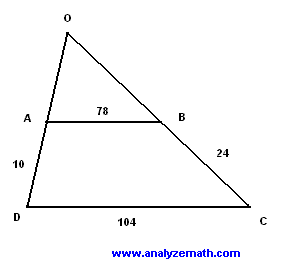
Solution to Problem 3
- Extend sides \( DA \) and \( CB \) to intersect at \( O \). Triangles \( AOB \) and \( DOC \) are similar:
\[ \frac{OA}{OD} = \frac{OB}{OC} = \frac{AB}{DC} = \frac{78}{104} = \frac{3}{4} \]
- Let \( OA = 3x \), \( OD = 4x \). Since \( OD = OA + 10 \):
\[ 4x = 3x + 10 \Rightarrow x = 10 \Rightarrow OA = 30,\; OD = 40 \]
- Let \( OB = 3y \), \( OC = 4y \). Since \( OC = OB + 24 \):
\[ 4y = 3y + 24 \Rightarrow y = 24 \Rightarrow OB = 72,\; OC = 96 \]
- Use Heron's formula for \( \triangle AOB \):
\[ s = \frac{30+72+78}{2} = 90 \]
\[ \text{Area} = \sqrt{90(90-30)(90-72)(90-78)} = 1080 \text{ units}^2 \]
- Use Heron's formula for \( \triangle DOC \):
\[ s = \frac{40+96+104}{2} = 120 \]
\[ \text{Area} = \sqrt{120(120-40)(120-96)(120-104)} = 1920 \text{ units}^2 \]
- Trapezoid area:
\[ \text{Area of } ABCD = 1920 - 1080 = 840 \text{ units}^2 \]
Additional Resources
Geometry Tutorials, Problems and Interactive Applets
Trapezoid Area Calculator
Trapezoid Calculator and Solver



