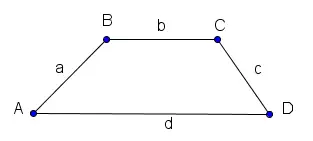
A trapezoid with bases \(b\) and \(d\) (with \(d > b\)), legs \(a\) and \(c\), and parallel sides \(AD\) and \(BC\) is shown below. Calculate all its angles and its height \(h\).

Using the trapezoid above, draw \(BB'\) parallel to \(CD\).

Using triangle \(ABB'\), apply the cosine rule:
\[ c^2 = a^2 + (d - b)^2 - 2a(d - b)\cos(\angle BAD) \]
\[ \cos(\angle BAD) = \frac{a^2 + (d - b)^2 - c^2}{2a(d - b)} \]
\[ \angle BAD = \arccos\left(\frac{a^2 + (d - b)^2 - c^2}{2a(d - b)}\right) \]
In the same figure, \(\angle BB'A\) and \(\angle CDA\) are equal.
Using triangle \(ABB'\) again:
\[ a^2 = c^2 + (d - b)^2 - 2c(d - b)\cos(\angle BB'A) \]
\[ \cos(\angle BB'A) = \frac{c^2 + (d - b)^2 - a^2}{2c(d - b)} \]
\[ \angle CDA = \angle BB'A = \arccos\left(\frac{c^2 + (d - b)^2 - a^2}{2c(d - b)}\right) \]
Since \(AD \parallel BC\), the pairs of angles are supplementary:
\[ \angle ABC = 180^\circ - \angle BAD, \quad \angle DCB = 180^\circ - \angle CDA \]
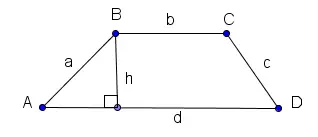
\[ h = a \sin(\angle BAD) = a \sin(\angle ABC) \]
\[ \text{Area} = \frac{1}{2}(b + d)h \]
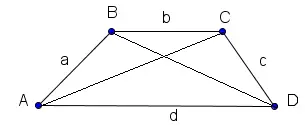
Apply the cosine rule in triangles \(DAB\) and \(BCD\):
\[ BD^2 = a^2 + d^2 - 2ad \cos(\angle BAD) \]
\[ BD = \sqrt{a^2 + d^2 - 2ad \cos(\angle BAD)} \]
\[ AC^2 = c^2 + d^2 - 2cd \cos(\angle CDA) \]
\[ AC = \sqrt{c^2 + d^2 - 2cd \cos(\angle CDA)} \]
Given: Bases \(d > b\), legs \(a\) and \(c\), with \(AD \parallel BC\).
Angles:
\(\displaystyle \angle BAD = \arccos\left(\frac{a^2 + (d - b)^2 - c^2}{2a(d - b)}\right)\)
\(\displaystyle \angle CDA = \arccos\left(\frac{c^2 + (d - b)^2 - a^2}{2c(d - b)}\right)\)
\(\angle ABC = 180^\circ - \angle BAD\)
\(\angle DCB = 180^\circ - \angle CDA\)
Height:
\(h = a \sin(\angle BAD)\)
Area:
\(\displaystyle A = \frac{1}{2}(b + d)h\)
Diagonals:
\(\displaystyle BD = \sqrt{a^2 + d^2 - 2ad \cos(\angle BAD)}\)
\(\displaystyle AC = \sqrt{c^2 + d^2 - 2cd \cos(\angle CDA)}\)