
Triangle geometry problems with step-by-step solutions.
The right triangle below has an area of \(25\). Find its hypotenuse.

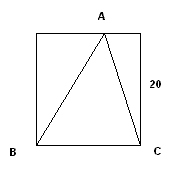
Triangle \(ABC\) is inscribed inside a square of side \(20\text{ cm}\). Find the area of the triangle.
Find the area of an equilateral triangle with side length \(10\text{ cm}\).
In an isosceles triangle, angle \(A\) is \(30^\circ\) greater than angle \(B\). Find all angles.
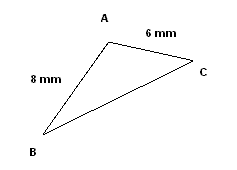
Triangle \(ABC\) has area \(15\text{ mm}^2\). Side \(AC = 6\text{ mm}\), side \(AB = 8\text{ mm}\), and \(\angle BAC\) is obtuse. Find \(\angle BAC\) and side \(BC\).
Points \(A(2,8)\) and \(B(2,3)\) share the same \(x\)-coordinate, so \(AB \parallel y\)-axis. Since \(BC \perp AB\), \(BC\) is horizontal with \(y_C = 3\).
Using area formula:
\[
25 = \frac{1}{2} \cdot AB \cdot BC = \frac{1}{2} \cdot 5 \cdot |x_C - 2|
\]
Solving: \(|x_C - 2| = 10 \Rightarrow x_C = 12\) (since \(C\) is left of \(B\)).
Hypotenuse \(AC = \sqrt{(12-2)^2 + (3-8)^2} = \sqrt{125} = 5\sqrt{5}\).
Base and height are both \(20\text{ cm}\): \[ \text{Area} = \frac{1}{2} \times 20 \times 20 = 200\text{ cm}^2. \]
For equilateral triangle with side \(s = 10\text{ cm}\), height: \[ h = \sqrt{10^2 - 5^2} = \sqrt{75} = 5\sqrt{3}\text{ cm} \] Area: \[ A = \frac{1}{2} \times 10 \times 5\sqrt{3} = 25\sqrt{3} \approx 43.3\text{ cm}^2. \]
Since \(\triangle ABC\) is isosceles with \(A > B\), then \(B = C\).
Given \(A = B + 30^\circ\) and \(A + B + C = 180^\circ\):
\[
(B + 30) + B + B = 180 \Rightarrow 3B = 150 \Rightarrow B = 50^\circ
\]
Thus: \(A = 80^\circ,\; B = C = 50^\circ\).
Using area formula: \[ 15 = \frac{1}{2} \cdot 6 \cdot 8 \cdot \sin A \Rightarrow \sin A = 0.625 \] Since \(A\) is obtuse: \[ A = 180^\circ - \arcsin(0.625) \approx 141.3^\circ \] By cosine rule: \[ BC^2 = 8^2 + 6^2 - 2 \cdot 8 \cdot 6 \cdot \cos 141.3^\circ \approx 174.97 \] \[ BC \approx \sqrt{174.97} \approx 13.23\text{ mm}. \]
Triangle Properties
Right Triangle Problems
Cosine Law Problems
Geometry Tutorials