Area and Volume of a Regular Polygon Frustum
Formulas Used in Calculator
Online calculator to calculate the total and lateral surface areas and the volume of a regular polygon frustum given the altitude and sides of the polygons or the radii of the circumcircle of the polygons..
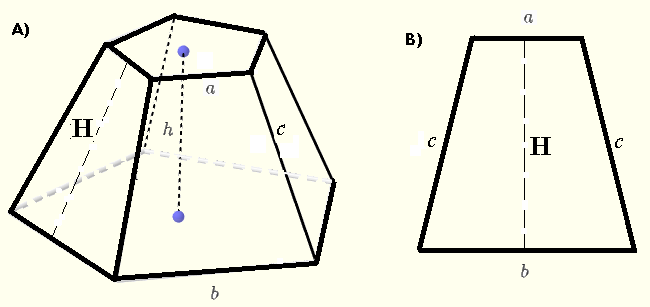
In figure A) below is shown the regular polygon frustum with similar regular polygons as bases. The upper base has side of length \( a \) and the lower base has side of length \( b \) and the two polygons have the same number of sides.
In figure B) is shown one face of the frustum which is an isosceles trapezoid where whose altitude is \( H \) which is also called the slant height of the frustum.
In figure C) is shown a top view of the frustum including the circumcircle of each polygon and with radii \( r_1 \) for the upper polygon and \( r_2 \) for the lower polygon.
In figure D) is shown the trapezoid made up of one edge of the frustum of length \( c \), the height of the frustum \( h \) and the radii \( r_1 \) and \( r_2 \).

Let \( A_1 \) be the area of the upper (regular polygon) base and \( A_2 \) be the area of the lower (regular polygon) base given by 1
\[ A_1 = \dfrac{1}{4} \; n \; a^2 \cot\left(\dfrac{180^{\circ}}{n}\right) \] and \[ A_2 = \dfrac{1}{4} \; n \; b^2 \cot\left(\dfrac{180^{\circ}}{n}\right) \]
The volume \( V \) of the regular polygon frustum is given by 1
\[ V = \dfrac{1}{3} (A_1+A_2 +\sqrt{A_1 A_2}) h\]
The area \(A_L\)of the lateral surface is given by
\[ A_L = \dfrac{1}{2} n (a+b) H \],
where
\[ H^2 = c^2 - \left(\dfrac{b-a}{2}\right)^2 \]
\[ c^2 = h^2 + (r_2-r_1)^2 \]
\[ r_1 = \dfrac{a}{2 \sin(\alpha/2)} \quad \text{and} \quad r_2 = \dfrac{b}{2 \sin(\alpha/2)}\]
\[ \alpha = \dfrac{360^{\circ}}{n} \]
How to Use the Calculator
Enter sides \( a \) and \( b \) of the upper and lower polygons, the height of the frustum \( h \), the number of sides \( n \) of each the polygon of the frustum and if necessary change the number of decimal places in the numerical results than press "Calculate". The outputs are the lateral surface area, the total surface area (including the base and bottom), the volume of the frustum and parameters x, y and angle t for the construction of a frustum given r, R and h.
The results are the areas of the upper and lower bases, the total volume, the area of the lateral surface and the total area, the slant height \( H \), the edge \( c \) and the radii of the circumcircles described above.
Results (wait, it takes time)
More References and Links
More Online Geometry Calculators and Solvers.
Regular Polygons Area
Frustum

