Kite Calculator
An online calculator to calculate the sides, area, perimeter and angles in a kite given its diagonals and distance \( AO \).
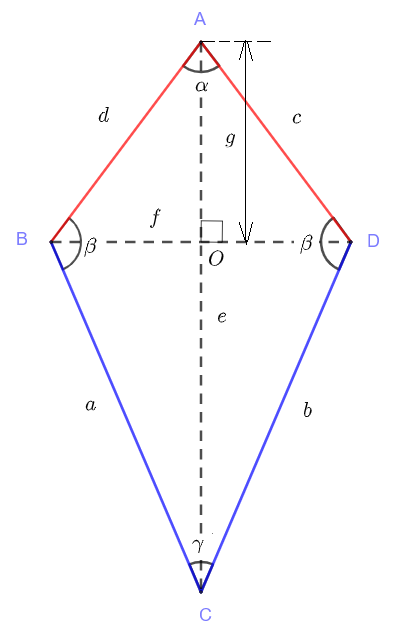
We define the length of segments \( AC \), \( BD \) and \( AO \) using small letters as follows: \( AC = e\), \( BD = f \) and \( AO = g \).
The kite formulas are first given.
Area \( A \) of Kite: \[ \displaystyle A = \dfrac{f \cdot e}{2} \]
Sides \( a \) and \( b \): \[ \displaystyle a = b = \sqrt{ \left(\dfrac{f}{2}\right)^2 + (e-g)^2} \]
Sides \( c \) and \( d \): \[ \displaystyle d = c = \sqrt{ \left(\dfrac{f}{2}\right)^2 + g^2} \]
Perimeter: \( \displaystyle p = 2 a + 2 d \)
Angle \( \alpha \): \[ \displaystyle \alpha = 2 \arctan (\dfrac{f}{2g}) \]
Angle\( \gamma \) : \[ \displaystyle \gamma = 2 \arctan \left(\dfrac{f}{2(e-g)}\right) \]
Angle \( \beta \): \[ \displaystyle \beta = 180 - \dfrac{\gamma}{2} - \dfrac{\alpha}{2} \]
Use of the Kite Calculator
Enter the lengths \( e \) of \( AC \), the length \( f \) of \( BD \) and the length \( g \) of \( AO \) as positive real numbers such that \( g \lt e \).Outputs
More References and links
Kite Questions with Solutions .Geometry Calculators
Geometry Tutorials, Problems and Interactive Applets
