Rectangular Pyramid Calculator and Maker
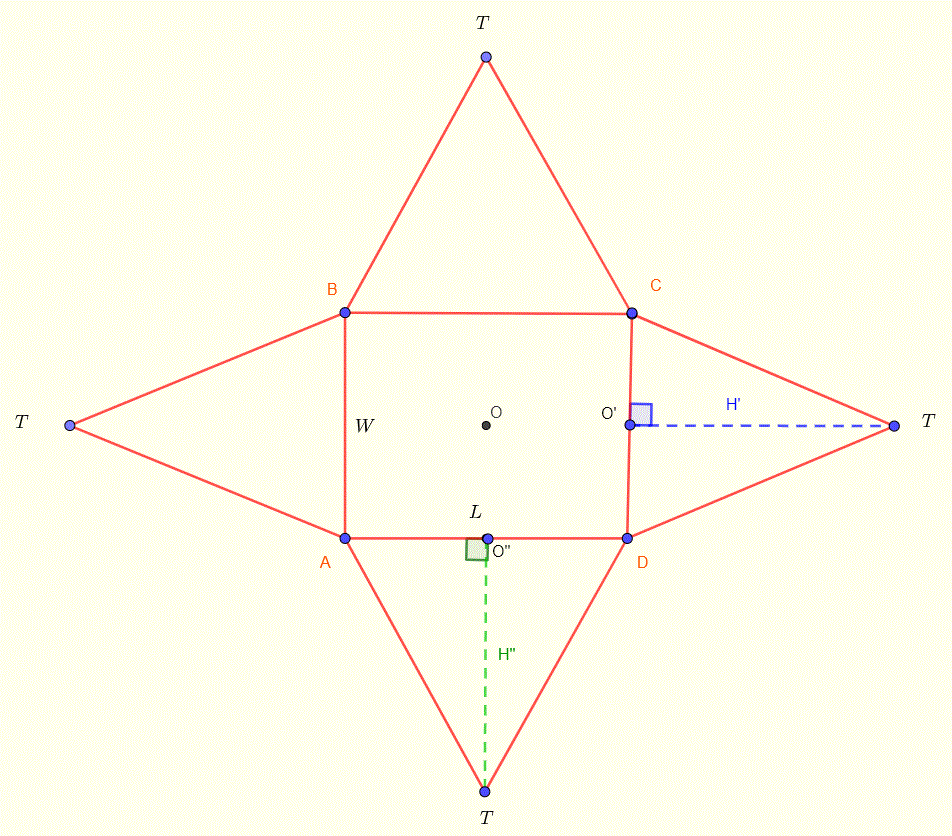
Online calculator to calculate the slant heights, surface area, the volume and many other parameters of a pyramid given the dimensions of its rectangular base and its height. The calculator gives all parameters necessary to make a pyramid with a rectangualr base. The net of the pyramid with all parameters to make it is shown at the bottom of the page.
Formulas of Area and Volume of the Pyramid Used in this Calculator
Let \( L \), \( W \) be the dimensions of a rectangular base of a pyramid and \( H \) its height.Area of rectangular base ABCD: \( A_b = L \times W \)
Slant height TO': \( H'= \sqrt{H^2+(L/2)^2} \) (length of TO' which is the altitude of triangle DTC )
Slant height TO'': \( H'' = \sqrt{H^2+(W/2)^2} \) (length of TO'' which is the altitude of triangle ATD )
Area of triangle (Face) DTC: \( A_{DTC} = \dfrac{1}{2} H' \times W \)
Area of triangle (Face) ATD: \( A_{ATD} = \dfrac{1}{2} H'' \times L \)
Total Area of Pyramid: \( A_T = A_b + 2 \times A_{DTC} + 2 \times A_{ATD} \) (area of base + twice area of triangle DTC + twice the area of triangle ATD)
Volume of Pyramid: \( V = \dfrac{1}{3} H \times A_b = \dfrac{L W H}{3}\)
Length of Edge TA = Length of Edge TB = Length of Edge TC = Length of Edge TD: \( S = \sqrt{H^2 + (W/2)^2 + (L/2)^2 } \)
Angle DTC = Angle ATB: \( \alpha = 2 \arcsin {\dfrac{W/2}{S}} \)
Angle ATD = Angle BTC: \( \beta = 2 \arcsin{\dfrac{L/2}{S}} \)
How to Use the Pyramid Calculator
Enter the length L and width W of the base of the pyramid and H the height of the pyramid as positive real numbers and press "calculate". The outputs are all parameters defined above
Dimensions and Net Needed to Make a Pyramid
The net of a pyramid with rectangular base is shown below. The length \( L \) and width \( W \) are given and the heights \( H' \) and \( H'' \) are calculated using the above calculator. Triangles ADT and BCT are congruent and triangles CDT and BAT are also congruent.
