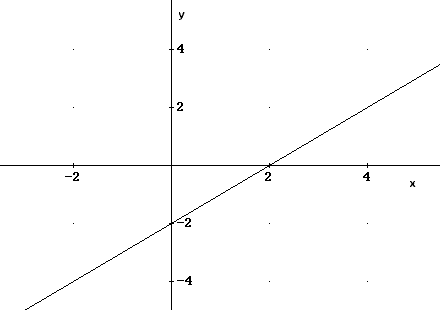Graph, Domain and Range of Absolute Value Functions

This is a step by step tutorial on how to graph functions with absolute value. Properties of the graph of these functions such as domain, range, x and y intercepts are also discussed. Free graph paper is available.

Graph, Domain and Range of Absolute Value Functions; Examples with Detailed Solutions

Example 1:

f is a function given by
\[ f (x) = |x - 2| \]

Find the x- and y-intercepts of the graph of \( f \).
Find the domain and range of \( f \).
Sketch the graph of \( f \).

Solution to Example 1

a - The y intercept is given by \[ (0 , f(0)) = (0 ,|-2|) = (0 , 2) \]
The x coordinate of the x intercepts is equal to the solution of the equation \[ |x - 2| = 0 \] which is \[ x = 2 \]
The x intercepts is at the point \( (2 , 0) \)
b - The domain of \( f \) is the set of all real numbers
Since \( |x - 2| \) is either positive or zero for \( x = 2 \); the range of \( f \) is given by the interval \[ [0 , +\infty) \].
c - To sketch the graph of \( f(x) = |x - 2| \), we first sketch the graph of \( y = x - 2 \) and then take the absolute value of \( y \).
The graph of \( y = x - 2 \) is a line with \( x \) intercept \( (2 , 0) \) and y intercept \( (0 , -2)\). (see graph below)
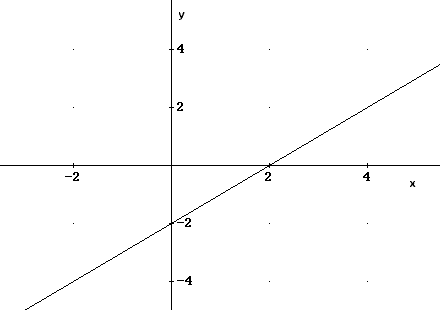
We next use the definition of the absolute value to graph \( f(x) = |x - 2| = | y | \).
If \( y \ge 0 \) then \( | y | = y \) , if \( y \lt 0 \) then \( | y | = -y \).
For values of \( x \) for which \( y \) is positive, the graph of \( | y | \) is the same as that of \( y = x - 2 \). For values of \( x \) for which \( y \) is negative, the graph of \( | y | \) is a reflection on the \( x \) axis of the graph of \( y \). The graph of \( y = x - 2 \) above has \( y \) negative on the interval \( (-\infty , 2) \) and it is this part of the graph that has to be reflected on the x axis. (see graph below).
Check that the range is given by the interval \( [0 , +\infty) \), the domain is the set of all real numbers, the y intercept is at \( (0 , 2) \) and the x intercept at \( (2, 0) \).

Example 2:

f is a function given by \[ f (x) = |(x - 2)^2 - 4| \]

Find the x- and y-intercepts of the graph of \( f \).
Find the domain and range of \( f \).
Sketch the graph of \( f \).

Solution to Example 2

a - The y intercept is given by \[ (0 , f(0)) = (0 ,(-2)^2 - 4) = (0 , 0) \]
The \( x \) coordinates of the x intercepts are equal to the solutions of the equation \[ |(x - 2)^2 - 4| = 0 \] which gives \[ (x - 2)^2 = 4 \] and the solutions are: \[ x = 0 \quad \text{and} \quad x = 4 \]
The x intercepts are at the points \( (0 , 0)\) and \( (4 , 0) \)
b - The domain of \( f \) is the set of all real numbers
Since \( |(x - 2)^2 - 4| \) is either positive or zero for \( x = 4 \) and \( x = 0 \); the range of \( f \) is given by the interval \[ [0 , +\infty) \]
c - To sketch the graph of \( f(x) = |(x - 2)^2 - 4| \), we first sketch the graph of \( y = (x - 2)^2 - 4 \) and then take the absolute value of\( y \).
The graph of \( y = (x - 2)^2 - 4 \) is a parabola with vertex at \( (2,-4) \), x intercepts at \( (0 , 0) \) and \( (4 , 0) \) and a y intercept \( (0 , 0) \). (see graph below)
The graph of \( f \) is given by reflecting on the x axis part of the graph of \( y = (x - 2)^2 - 4 \) for which \( y \) is negative. (see graph below).