Graphing arcsin(x) functions

A step by step tutorial on graphing and sketching arcsin functions where also the domain and range of these functions and other properties are discussed.

Graph, Domain and Range of arcsin(x)

In what follows, \( \arcsin(x) \) is the inverse function of \( f(x) = sin(x) \) for \( -\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2} \).
The domain of \( y = \arcsin(x) \) is the range of \( f(x) = \sin(x) \) for \( -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \) and is given by the interval \([-1, 1]\).
The range of \(\arcsin(x)\) is the domain of \( f \) which is given by the interval \([-\frac{\pi}{2}, \frac{\pi}{2}]\).
The graph, domain and range of both \( f(x) = \sin(x) \) for \( -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \) and \(\arcsin(x)\) are shown below.

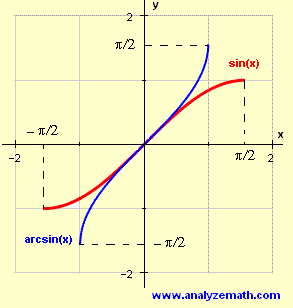
graph of sin(x) and arcsin(x)

A table of values of \( \arcsin(x) \) can made as follows: \[ \begin{array}{|c|c|c|c|} \hline x & -1 & 0 & 1 \\ \hline y = \arcsin(x) & -\frac{\pi}{2} & 0 & \frac{\pi}{2} \\ \hline \end{array} \]

Note that there are 3 key points that may be used to graph \(\arcsin(x)\). These points are: \((-1,-\frac{\pi}{2})\) , \((0,0)\) and \((1,\frac{\pi}{2})\).

Example 1

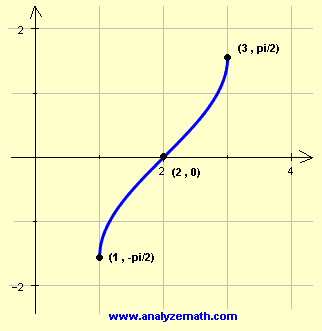
Find the domain, range and graph the function \[ y = \arcsin(x - 2) \].

Solution to Example 1

The graph of \( y = \arcsin(x - 2) \) will be that of \( \arcsin(x) \) shifted 2 units to the right. The domain is found by stating that \( -1 \leq x - 2 \leq 1 \). Solve the double inequality to find the domain: \[ 1 \leq x \leq 3 \] The 3 key points of \( \arcsin(x) \) can also be used in this situation as follows: \[ \begin{array}{|c|c|c|c|} \hline x - 2 & -1 & 0 & 1 \\ \hline y = \arcsin(x - 2) & -\frac{\pi}{2} & 0 & \frac{\pi}{2} \\ \hline x & 1 & 2 & 3 \\ \hline \end{array} \] The value of \( x \) is calculaed from the value of \( x - 2 \). For example, when \( x - 2 = -1 \), solve for \( x \) to find \( x = 1 \) and so on.
The domain is given by the interval \( [1, 3] \) and the range is given by the interval \( \left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \).
The three points will now be used to graph \( y = \arcsin(x - 2) \).

Example 2

Find the domain and range and graph the function: \[ y = 2 \arcsin(x + 1) \]

Solution to Example 2
We use the 3 key points in the table as follows, then find the value \( y = 2 \arcsin(x + 1) \) and \( x \).
\[ \begin{array}{|c|c|c|c|} \hline x + 1 & -1 & 0 & 1 \\ \hline \arcsin(x + 1) & -\frac{\pi}{2} & 0 & \frac{\pi}{2} \\ \hline y = 2\arcsin(x + 1) & -\pi & 0 & \pi \\ \hline x & -2 & -1 & 0 \\ \hline \end{array} \]
domain is : \[ [-2,0] \] , range is: \[ [- \pi , \pi] \]

graph of y = 2arcsin(x+1)

The graph is that of arcsin(x) shifted one unit to the left and stretched vertically by a factor of 2.

Example 3

Find the domain and range and graph the function: \[ y = - \arcsin(x - 1) \]

Solution to Example 3

We use the 3 key points in the table as follows, then find the value \( - \arcsin(x - 1) \) and \( x \).
\[ \begin{array}{|c|c|c|c|} \hline x - 1 & -1 & 0 & 1 \\ \hline \arcsin(x - 1) & -\frac{\pi}{2} & 0 & \frac{\pi}{2} \\ \hline y = -\arcsin(x - 1) & \frac{\pi}{2} & 0 & -\frac{\pi}{2} \\ \hline x & 0 & 1 & 2 \\ \hline \end{array} \]
domain is: \[ [0 , 2] \] , range is: \[ [- \frac{\pi}{2} , \frac{\pi}{2} \]

graph of y = -arcsin(x-1)

The graph is that of \( \arcsin(x) \) shifted one unit to the right and reflected on the x axis.