Graphing by Translation, Scaling and Reflection

A step by step tutorial on the properties of transformations such as vertical and horizontal translation (or shift) , scaling and reflections on x-axis and y-axis of graphs of functions is presented.

Translation / Shifting Horizontally

For any function \(f(x)\), if we replace \(x\) with \(x + c\), the graph of \(f(x + c)\) will be the graph of \(f(x)\) shifted horizontally by \(c\) units. More specifically: \[ f(x + c) \text{ is the graph of } f(x) \text{ shifted } c \text{ units to the left for } c \gt 0 \] Or equivalently: \[ f(x - c) \text{ is the graph of } f(x) \text{ shifted } c \text{ units to the right for } c \gt 0 \] The example of the graph of f(x) = x² and g(x) = (x - 2)² are shown below and it is easily seen that the graph of (x - 2)² is that of x² shifted 2 units to the right. The example of the graph of \( f(x) = x^2 \) and \( g(x) = (x - 2)^2 \) are shown below, and it is easily seen that the graph of \( (x - 2)^2 \) is that of \( x^2 \) shifted 2 units to the right.

\[ \begin{array}{c@{\hspace{4cm}}c} \text{\( f(x) = x^2 \)} \quad & \quad \text{\( g(x) = (x - 2)^2 \)} \\ \end{array} \]

Graph of Quadratic Function (Parabola) Translated Horizontally to Right

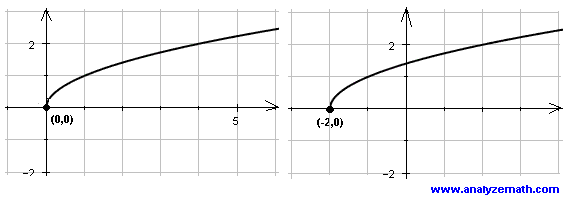
If \( c \) is positive, then the graph is shifted to the left. The example of the graph of \( f(x) = \sqrt{x} \) and \( g(x) = \sqrt{x + 2} \) are shown below, and it is easily seen that the graph of \( \sqrt{x + 2} \) is that of \( \sqrt{x} \) shifted 2 units to the left.

\[ \begin{array}{c@{\hspace{4cm}}c} \text{\( f(x) = \sqrt{x} \)} \quad & \quad \text{\( g(x) = \sqrt{x + 2} \)} \\ \end{array} \]

Graph of Square Root Function Translated Horizontally to Left

Translation / Shifting Vertically

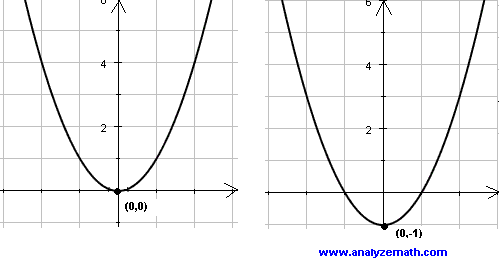
If we add a constant \( c \) to \( f(x) \), the graph of \( f(x) + c \) will be the graph of \( f(x) \) translated (or shifted) vertically. If \( c \) is positive, the graph is translated up. If \( c \) is negative , the graph is translated down; as shown in the graph below. \[ \begin{array}{c@{\hspace{3cm}}c} f(x) = x^2 \quad & \quad g(x) = x^2 + 2 \end{array} \]

Graph of Quadratic Function Translated Vertically Up

If \( c \) is negative, the graph is translated down as shown in the graph below.

\[ \begin{array}{c@{\hspace{3cm}}c} f(x) = x^2 \quad & \quad g(x) = x^2 - 1 \end{array} \]

Graph of Quadratic Function Translated Vertically Down

Reflection on y-axis

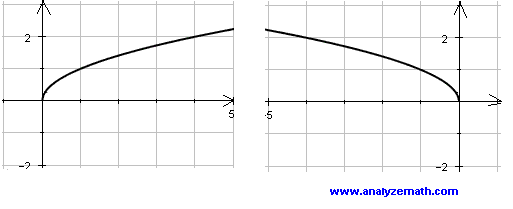
Take any function f(x) and change x to - x, the graph of f(- x) will be the graph of f(x) reflected on the y axis. \[ \begin{array}{c c} f(x) = \sqrt{x} \quad & \quad g(x) = \sqrt{-x} \end{array} \]

Graph of Absolute Value Function Reflected on y-axis

Reflection on x-axis

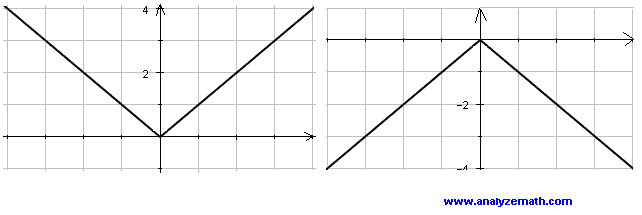
Take any function \( f(x) \) and it to \( - f(x) \), the graph of \( - f(x) \) will be the graph of \( f(x) \) reflected on the x axis.

\[ \begin{array}{c@{\hspace{3cm}}c} f(x) = |x| \quad & \quad g(x) = -|x| \\ \end{array} \]

Graph of Absolute Value and Its Reflection

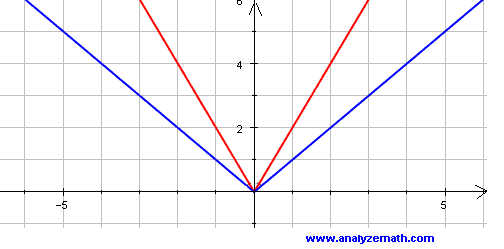
Scaling Vertically

Take any function \( f(x)\), the graph of \( k f(x) \) (with \( k \gt 0 \)) will be the graph of \( f(x) \) expanded vertically if \( k \) is greater than \( 1 \) and compressed vertically if \( k \) is less than \( 1 \).

Graph in blue is that of f(x) = |x| and the graph in red is that of g(x) = 2 |x|

Graph of Absolute Value Function Scaled Vertically