Free Mathematics Tutorials

BC Calculus Test Practice Questions with Answers
Sample 1

A set of BC calculus questions, with answers, similar to the questions in the AP calculus test are presented. The answers to the suggested questions are at the bottom of the page.

If dy / dx = (2x - 1)y , y(1) = e, find y(2).
A) 3 e
B) 3^e
C) e / 3
D) 3 / e
E) e³
A particle moves along the x-axis with a velocity v given by v(t) = 2t² - t + 1. When t = 0, the particle is at x = -3. Find the position along the x axis of the particle at t = 2.
A) 7
B) 7 / 3
C) 1
D) 22
E) 3 / 7
Evaluate the integral

A) 0
B) ln(7/3) + ln(2)
C) 2 ln(7/3) - ln(2)
D) 2 ln(7/3) + ln(2)
E) 3 ln(7/3)
Evaluate the integral

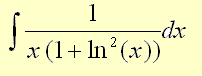
A) atan(ln(x)) + C
B) 0.5 x²(ln²(x) ln(x)) + (3/4)(x²) + C
C) [ 0.5 x²(ln²(x) ln(x)) + (3/4)(x²) ]^-1 + C
D) asin(ln(x)) + C
E) 1 / atan(ln(x)) + C
If function f is defined by f(x) = 2 + ln(x + 3), the inverse function of f is given by
A) f^-1(x) = (2 + ln(x + 3))^-1
B) f^-1(x) = ln(x - 2)
C) f^-1(x) = - (2 + ln(x + 3))^-1
D) f^-1(x) = e^{x - 2} - 3
E) f^-1(x) = e^{x + 2} - 3
If f is a function such that f'(x) < 0 and f"(x) < 0 for all x, which of the following would be the graph of f?
The set of all values of K so that the graph of f(x) = x⁴ - 14x² + 24x + K has two distinct x intercepts is given by
A) (0 , +infinity)
B) (-infinity , +infinity)
C) (-100, -11) U (-11 , 130)
D) (-8 , 127)
E) (-infinity , -11) U (-8 , 117)
Function f is such that f(-x) = f(x) and differentiable for all x. Which of the following must be true
A) f '(-x) = 1/f '(x)
B) f '(-x) = f '(x)
C) f '(-x) = -f '(x)
D) f '(-x) = -1/f '(x)
E) f '(-x) = (f '(x))^-1
If y = x^{x + 1}, then y' =
A) (x + 1) x^x
B) (x + 1) x^{x - 1}
C) x ln(x^x) + x + 1
D) x^x (x ln(x) + x + 1)
E) x^x x ln(x)
If x = ln(t + 1) and y = ln (t + 2), then dy/dx =
A) 1
B) (t + 1) / (t + 2)
C) (t + 2) / (t + 1)
D) 1 / (t + 2)ln(t + 1) - ln(t + 2)/(t + 1)ln(t + 1)²
E) 1 / (t + 2)
A) 1
B) 2
C) 0
D) -2
E) -1
If y = sin(sin(sin(x))), then dy/dx =
A) cos(sin(sin(x)))
B) cos(cos(sin(x)))
C) cos(x) cos(sin(x)) cos(sin(sin(x)))
D) cos(cos(cos(x)))
E) cos(x) cos(sin(x)) cos(cos(sin(x)))
Find dy/dx if x = ln(y - e^-y)
A) (y + e^-y)
B) (y - e^-y) / (1 - e^-y)
C) (y + e^-y) / (1 - e^-y)
D) (y - e^-y) / (1 + e^-y)
E) (y - e^-y)
Find dy/dx where x and y are related by the parametric equations: x = ln(t) + t and y = t - ln(t)
A) (t - 1) / (t + 1)
B) (t + 1) / (t - 1)
C) -(t - 1) / (t + 1)
D) -(t + 1) / (t - 1)
E) 1
f, g and h are differentiable functions such that g(x) = f(h(x)), f(0) = 1, h(0) = 2, g'(0) = 3, f'(0) = 7, f'(2) = 6 and f'(5) = 8. Find h'(0).
A) 2
B) 1/2
C) -1/2
D) 1
E) -1
If f and g are functions such that f(g(x)) = 2x and f(t) = e^{2t + 1}, then then g(x) =
A) ln(2x)
B) e^2x
C) ln(2x) + 1
D) (ln(2x) - 1) / 2
E) ln(x)
In the figure below, half a period of sin(x) from 0 to Pi is split into two regions (yellow and green) of equal area by a line through the origin. The line and the sine function intersect at a point whose x coordinate is K. What equation does K satisfy?

A) sin(K) = K
B) cos(K) = K sin(K)
C) K cos(K) = sin(K)
D) (2 + K) sin(K) + 2 cos(K) = 0
E) K sin(K) + 2 cos(K) = 0
Which of the following graphs is that of the polar curve defined by r = -csc(t)
Find dy/dx if y = | x² + 2x - 1 |.
A) (2x + 2) (x² + 2x - 1) / | x² + 2x - 1 |
B) |2x + 2|
C)-|2x + 2|
D) |2x - 2|
E) -2x + 2
If f(x) = x⁵ + 5 x⁴ - 40 x² - 80 x - 48, which is true about the graph of f?
A) it has no x intercepts
B) it has 3 points of inflection
C) it is concave up for all x
D) it has 1 point of inflection
E) it has 2 points of inflection