A set of BC calculus questions, with answers, similar to the questions in the AP calculus test are presented. The answers to the suggested questions are at the bottom of the page.

1. 
   If x + y = e^{(x + y)}, then the value of dy/dx at the point (1/2 , 1/2) is
   A) 1
   B) e - 1
   C) 1 - e
   D) e
   E) -1
2. 
   Evaluate the integral
   
   A) 0
   B) 1
   C) 2
   D) -1
   E) -2
3. 
   The acceleration a(t) of a body in motion along a straight line is given by a(t) = 2t - 4, where t is the time. If x(t) is the distance of the body from the origin at the time t and x(6) - x(2) = 10, then the velocity v(t) of the body is given by
   A) t² - 4t
   B) t² - 4t + 7/6
   C) t
   D) t²
   E) 2t² - 4t
4. 
   Evaluate
   
   A) 1
   B) e
   C) e - 1
   D) e + 1
   E) 0
5. 
   Which of these series is/are convergent?
   
   A) A only
   B) B only
   C) A, B and C
   D) A and B only
   E) B and C only
6. 
   Evaluate
   
   A) ln(3/4)
   B) ln(2)
   C) 1
   D) -ln(2)
   E) ln(2)
7. 
   What is true about the graph of f(x) = ln(x² + 2x + 1)?
   A) It has no x intercept
   B) It has a horizontal asymptote
   C) It is exactly the same as the graph of g(x) = 2 ln| x + 1 |
   D) It is exactly the same as the graph of g(x) = 2 ln(x + 1)
   E) It has no y intercept
8. 
   For what value of C we have the following
   
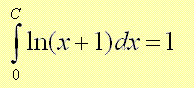
   A) e
   B) e - 1
   C) 1 - e
   D) 1
   E) 2e
9. 
   Find constant K, K positive, so that the volume of the solid of revolution determined by rotating the area bounded by f(x) = x² and g(x) = - x(x - K) is equal to 200 Pi.
   A) 4 ^. 5^2/3
   B) 1 / 2
   C) 120
   D) ^. 1200^1/5
   E) 2 ^. 600^1/5

Answers to the Above Questions

1. E
2. A
3. B
4. C
5. D
   
6. D
7. C
8. B
9. E