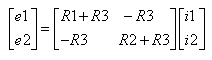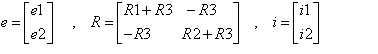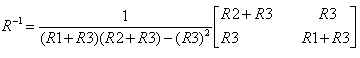
A tutorial on how mathematics, matrices in particular, are applied to model electric circuits.
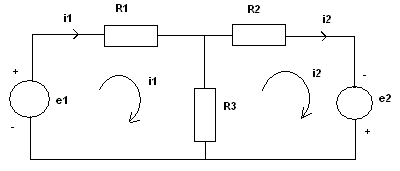
There are two closed loops in the above circuit. loop 1: e1, R1 and R3 and loop 2: e2, R2 and R3. e1 and e2 are sources of voltages. R1, R2 and R3 are resistors. i1 is the current flowing across R1 and i2 is the current flowing across R2. We now apply Kirchhoff's law to each loop.
loop 1: e1 = R1 i1 + R3 (i1 - i2)
loop 2: e2 = R2 i2 + R3 (i2 - i1)
Question: If e1, e2, R1, R2 and R3 are known, how do you calculate i1 and i2? This circuit is simple and involves only two equations. However electric circuits can be much more complicated that the one above and matrices are suitable to answer the above question. Let us group like terms in the above system of equations
e1 = i1 (R1 + R3) - i2 R3
e2 = - i1 R3 + i2(R2 + R3)
and then write it in matrix form as follows
The above is a matrix equation that may be solved using any known method to solve systems of equations. Let e, R and i be matrices given by
The solution to the above matrix equation is given by
More Mathematics Applied to Physics and Engineering.
