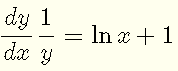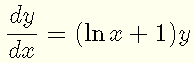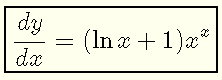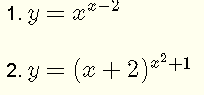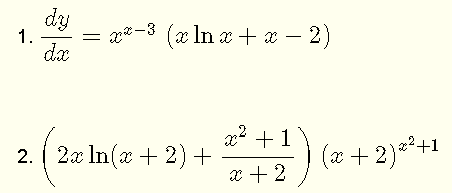Find The Derivative of x x
Find the first derivative of y = x x for x > 0 with all the steps presented.
Derivative of x x with Steps
Note that the function y = x x is neither a power function of the form x k nor an exponential function of the form b x and the known formulas of
Differentiation of these two functions
cannot be used. We need to find another method to find the first derivative of the given function.
Given
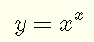
Take the natural log (ln) of both sides of the above
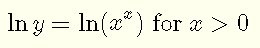
Use properties of logarithmic functions ln Ab = b ln A to the right side of the above equation and obtain
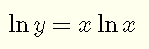
Differentiate both sides of the above with respect to x , using the chain rule on the left side and the product rule on the right.
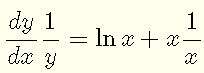 Simplify the right side
Simplify the right side
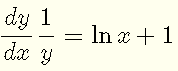
Multiply both sides by y and simplify
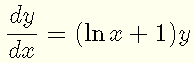
Substitute y by x x to obtain the final answer
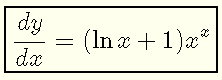
Exercises
Find the first derivative of
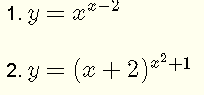
Answer to the Above Exercise:
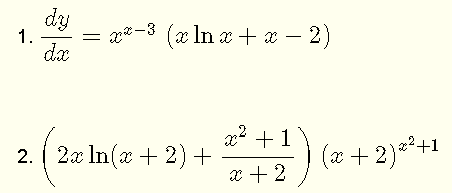
More References and Links
differentiation and derivatives
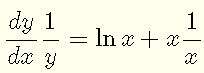 Simplify the right side
Simplify the right side