Find The Volume of a Square Pyramid Using Integrals
Find the formula for the volume of a square pyramid using integrals in calculus.
Problem : A pyramid is shown in the figure below. Its base is a square of side a and is orthogonal to the y axis. The height of the pyramid is H. Use integrals and their properties to find the volume of the square pyramid in terms of a and H.
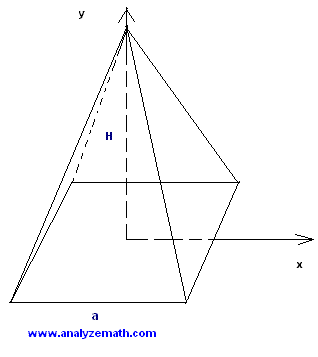
Solution to the problem: Let us first position the pyramid so that two opposite sides of the square base are perpendicular to the x axis and the center of its base is at the origin of the x-y system of axes. If we look at the pyramid in a direction orthogonal to the x-y plane, it will look like a two dimensional shape as shown below. AC is the slant height. 
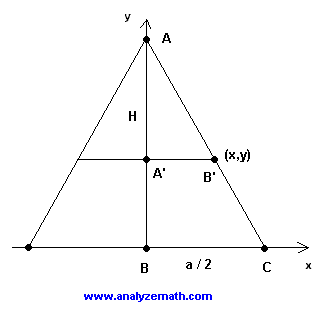
Let x = A'B' be the length of half of the side of the square at height y. The area A of the square at height y is given by: A(x) = (2x)2 The volume is found by adding all the volumes A dy that make the pyramid from y = 0 to y = H. Hence Volume =  0H A 2 dy
= 4 0H x 2 dy
We now use the fact that triangles ABC and AB'C' are similar and therefore the lengths of their corresponding sides are proportional to write: (a/2) / x = H / (H - y) We now solve the above for x to obtain x = a (H - y) / (2 H) We now substitute x in the integral that gives the volume to obtain Volume = 4 (a/2H)2 0H(H - y) 2 dy
Let us define t by t = H - y and dt = - dy The volume is now given by Volume = 4 (a/2H)2 H0t 2 (- dt)
Evaluate the integral and simplify Volume = 4 (a/2H)2 [H3 / 3] Volume = a2 H / 3 The volume of a square pyramid is given by the area of the base times the third of the height of the pyramid. More references on integrals and their applications in calculus. Area under a curve. Area between two curves. Find The Volume of a Solid of Revolution. Volume by Cylindrical Shells Method. |
