First, Second Derivatives and Graphs of Functions

A tutorial on how to use the first and second derivatives, in calculus, to study the properties of the graphs of functions.

Theorems

To graph functions in calculus we first review several theorem. 3 theorems have been used to find maxima and minima using first and second derivatives and they will be used to graph functions. We need 2 more theorems to be able to study the graphs of functions using first and second derivatives.
Theorem 4: If f is differentiable on an interval (I1 , I2) and differentiable on [I1 , I2] and
4.a - If f ' (x) > 0 on (I1 , I2) , then f is increasing on [I1 , I2].
4.b - If f ' (x) < 0 on (I1 , I2) , then f is decreasing on [I1 , I2].
4.c - If f ' (x) = 0 on (I1 , I2) , then f is constant on [I1 , I2].
Theorem 5: If f is twice differentiable on an interval (I1 , I2) and
5.a - If f '' (x) > 0 on (I1 , I2) , then f has concavity up on [I1 , I2].
5.b - If f ' (x) < 0 on (I1 , I2) , then f is concavity down [I1 , I2].

Examples with Detailed Solutions

We will present examples of graphing functions using the theorems in "using first and second derivatives" and theorems 4 and 5 above.

Example 1

Use first and second derivative theorems to graph function f defined by
f(x) = x²
Solution to Example 1.
step 1: Find the first derivative, any stationary points and the sign of f ' (x) to find intervals where f increases or decreases.
f ' (x) = 2x
The stationary points are solutions to:
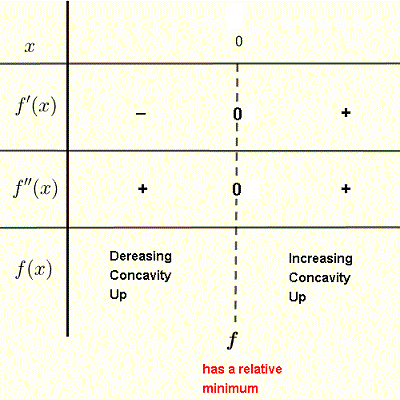
f ' (x) = 2x = 0 , which gives x = 0. The sign of f ' (x) is given in the table below. f ' (x) is negative on (-? , 0) f decreases on this interval. f ' (x) is positive on (0 , ?) f increases on this interval. Also according to theorem 2(part a) "using first and second derivatives", f has a minimum at x = 0.

step 2: Find the second derivative, its signs and any information about concavity.
f ''(x) = 2 and is always positive (this confirms the fact that f has a minimum value at x = 0 since f ''(0) = 2, theorem 3(part a)), the graph of f will be concave up on (-? , +?) according to theorem 5(part a) above.
step 3: Find any x and y intercepts and extrema.
y intercept = f(0) = 0.
x intercepts are found by solving f(x) = x² = 0. x intercept = 0.
From the signs of f ' and f'', there is a minimum at x = 0 which gives the minimum point at (0 , 0).
step 4: Put all information in a table and graph f.
Also as x becomes very large (+?) or veyy small (-?) , f(x) = x² becomes very large.
See table above and graph below.

Example 2

Use first and second derivative theorems to graph function f defined by
f(x) = x³ - 4x² + 4x
Solution to Example 2.
step 1: f ' (x) = 3x² - 8x + 4.
Solve 3x² - 8x + 4 = 0
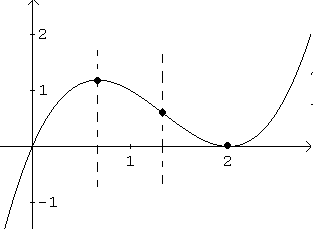
solutions are: x = 2 and x = 2/3, see table of sign below that also shows interval of increase/decrease and maximum and minimum points.
step 2: f '' (x) = 6x - 8.
Solve 6x - 8 = 0 ; solution is x = 4/3 inflection point: where concavity changes. See sign and concavity in table below.
step 3: y intercept = f(0) = 0. x intercepts solve x³ - 4x² + 4x = 0.
factor x out x(x² - 4x + 4) = 0 and solve the quadratic equation x² - 4x + 4 = (x - 2)² = 0 to find solutions: x = 0, x = 2 of multiplicity 2.
Also as x becomes very large (+?) , f(x) = x³ - 4x² + 4x becomes very large (+?). As x becomes very small (-?), f(x) becomes very small (-?).
step 4: The table and the graph are shown below.