Maximum Area of Triangle - Optimization Problem with Solution
The first derivative is used to maximize the area of a triangle inscribed in a circle. An optimization problem with solution.
Problem
In the picture below triangle ABC is inscribed inside a circle of center O and radius r. For a constant radius r of the circle, point B slides along the circle so that the area of ABC changes. Find the length of sides AB and CB so that the area of triangle ABC is maximum.
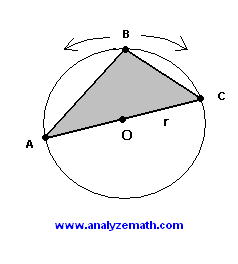
Solution to Problem:
Since the center O of the circle is on the side AC of the triangle, AC is a diameter of the circle and triangle ABC is a right triangle (Thales's theorem). Its right angle is at B and its hypotenuse AC has length equal to \(2r\).(see figure below)

The area \(S\) of the triangle is given by
\[ S = \frac{1}{2} AB \times CB \]
Using angle \(t\), \(AB\) and \(CB\) may be expressed as follows
\[ AB = AC \times \cos t \quad \text{and} \quad CB = AC \times \sin t \]
Substitute \(AC\) by \(AC \times \cos t\) and \(CB\) by \(AC \times \sin t\) in the above formula for the area, we obtain
\[ S = \frac{1}{2} AC^2 \cos t \sin t \]
We now use the trigonometric formula \(\sin(2t) = 2 \sin t \cos t\) to express the area \(S\) as follows.
\[ S = \frac{1}{4}AC^2 \sin(2t) \]
Since the radius \(r\) is constant, the length of the diameter \(AC\) is also constant, hence the area depends on angle \(t\) only as point B slides along the circle. To find \(t\) so that \(S\) is maximum, we need to find the first derivative and the stationary points.
\[ \frac{dS}{dt} = \frac{1}{4}AC^2 2 \cos(2t) \]
We now equate \(\frac{dS}{dt}\) to zero to find stationary points and interval of increase and decrease.
\[ \frac{1}{4}AC^2 2 \cos(2t) = 0 \]
As point B slides along the circle, angle \(t\) changes from 0 to 90 degrees. So the only solution to the above equation in the interval \( (0 , 90) \) is
\[ 2t = 90 \quad \text{or} \quad t = 45 \text{ degrees} \]
As \(t\) changes from 0 to 45 , \(2t\) changes from 0 to 90 and \(\frac{dS}{dt}\) is positive on this interval. As \(t\) changes from 45 to 90, \(2t\) changes from 90 to 180 degrees and \(\frac{dS}{dt}\) is negative on this interval. \(t = 45\) degrees is the location of a maximum value for the area \(S\).
When \(t = 45\) degrees, the area of the inscribed right triangle is maximum. The length of sides \(AB\) and \(CB\) are given by
\[ AB = AC \times \cos (45 \text{ degrees}) = 2r \sqrt{2} \]
and
\[ CB = AC \times \sin (45 \text{ degrees}) = 2r \sqrt{2} \]
The area is maximum when \(t = 45\) degrees which also means that the right triangle is isosceles.
References and Links
calculus problems


