Maximum Radius of Circle
Optimization Problem with Solution

Use the derivative to find the size of an angle of a right triangle so that the radius of the circle inscribed is maximum; for a constant hypotenuse.

Problem

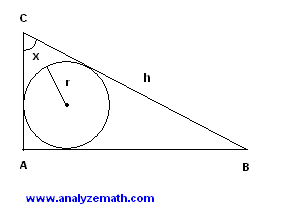
Solution to Problem:

• a) Let M, N and P be the points of tangency of the circle and the sides of the triangle. OM, ON and OP are perpendicular to CB, CA and AB respectively.
  

  

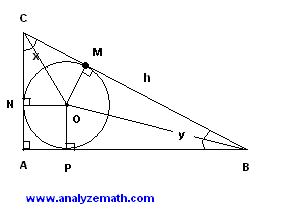
• Triangles COM and CON are rigth triangles and have two congruent sides: CO and OM and ON; the two triangles are therefore congruent. We denote the size of angle MCN by x and write
  tan(x / 2) = r / CM
  
• Triangles BOM and BOP are rigth triangles and have two congruent sides: BO and OM and OP; the two triangles are therefore congruent. We denote the size of angle MBP by y and write
  tan(y / 2) = r / BM
  
• Note that
  y + x = 90 which gives y / 2 = 45 - x / 2
  
• Substitute y / 2 by 45 - x / 2 in the equation tan(y / 2) = r / BM to obtain
  tan(45 - x / 2) = r / BM
  
• We now solve the equation tan(x / 2) = r / CM for CM
  and solve equation tan(45 - x / 2) = r / BM for BM to obtain
  CM = r / tan(x/2) and BM = r / tan(45 - x/2)
  
• We now use the fact that h = CM + BM to write the equation
  h = r / tan(x/2) + r / tan(45 - x/2)
  = r [ 1 / tan (x/2) + 1 / tan(45 - x/2) ]
  
• We now use trigonometric identities to simplify the above equation. The first identity we will use is
  tan(45 - x/2) = ( tan(45) - tan(x/2) ) / ( 1 + tan(45)tan(x/2) )
  = ( 1 - tan(x/2) ) / ( 1 + tan(x/2) )
  
• The formula for h is now given by
  h = r [ 1 / tan (x/2) + (1 - tan(x/2)) / ( 1 + tan(x/2)) ]
  
• We now use the identity tan(x/2) = sin(x/2) / cos(x/2) and other identities to rewrite h as follows
  h = r [ cos(x/2) / sin(x/2) + (cos(x/2) + sin(x/2)) / (cos(x/2) - sin(x/2)) ]
  = r [ 1 / [ (sin(x/2) (cos(x/2) - sin(x/2)) ] ]
  
• We now solve the above equation for r to obtain
  r = h sin(x/2) ( cos(x/2) - sin(x/2) ) = h ( sin(x/2) cos(x/2) - sin ²(x/2))
  
• We now use the identities sin(x/2)cos(x/2) = (1/2) sin (x) and sin ²(x/2) = 1/2 - (1/2)cos(x) to write r as follows
  r = (h / 2) ( sin(x) + cos(x) - 1)
  
• b) Now that we have calculated r as a function of x, and h assumed constant, let us find the first derivative of r with respect to x
  dr / dx = (h / 2) [ cos(x) - sin(x)]
  
• Let us find a critical points for r by solving the equation dr / dx = 0.
  (h / 2) [ cos(x) - sin(x)] = 0
  
• gives
  cos(x) - sin(x) = 0 since h is constant and not equal to 0.
  cos(x) = sin(x)
  
• Square both sides
  cos ²(x) = sin ²(x)
  cos ²(x) = 1 - cos ²(x)
  
• Solve for cos x to obtain
  cos(x) = + 1/√(2) or - 1/√(2)
  
• x is a acute angle and therefore the solution to our equation is given by
  x = π/4 = 45 degrees.
  
• The graph of dr/dx is shown below and dr/dx is positive for x < π/4 and negative for x > π/4, therefore r has a maximum at x = π/4 = 45 degrees.

  

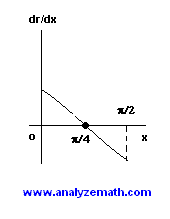
• x = 45 degrees is the value of angle ACB for which the radius r is maximum for a given value h of the length of the hypotenuse. Note that in this case triangle ABC is isosceles.