Use Derivatives to solve problems: Distance-time Optimization
A problem to minimize (optimization) the time taken to walk from one point to another is presented. An analytical method, using derivatives and other calculus concepts and theorems, is developed in order to find an analytical solution to the problem.
Problem
You decide to walk from point A (see figure below) to point C. To the south of the road through BC, the terrain is difficult and you can only walk at \(3 \, \text{km/hr}\). However, along the road BC you can walk at \(5 \, \text{km/hr}\). The distance from point A to the road is \(5 \, \text{km}\). The distance from B to C is \(10 \, \text{km}\). What path you have to follow in order to arrive at point C in the shortest (minimum) time possible?
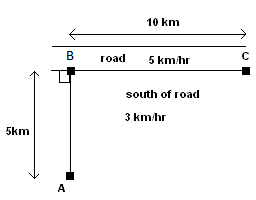
Solution to the Problem
Let us suppose that you follow the path from A to P and from P to C along straight lines.
We now look at a solution using derivatives and other calculus concepts. Let distance BP be equal to \(x\). Let us find a formula for the distances AP and PC. Using Pythagorean theorem, we can write:
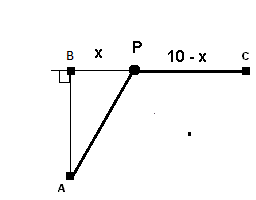
distance AP = \(\sqrt{5^2 + x^2}\)
distance PC = \(10 - x\)
We now find time \(t_1\) to walk distance AP. (time = distance / speed).
\(t_1 = \dfrac{\sqrt{5^2 + x^2}}{3}\)
Time \(t_2\) to walk distance PC is given by
\(t_2 = \dfrac{10 - x}{5}\)
The total time \(t\) is found by adding \(t_1\) and \(t_2\).
\(t = \dfrac{\sqrt{5^2 + x^2}}{3} + \dfrac{10 - x}{5}\)
we might consider the domain of function \(t\) as being all values of \(x\) in the closed interval \([0 , 10]\). For values of \(x\) such that point \(P\) is to the left of \(B\) or to the right of \(C\), time \(t\) will increase.
To find the value of \(x\) that gives \(t\) minimum, we need to find the first derivative \(\dfrac{dt}{dx}\) (\(t\) is a functions of \(x\)).
\(\dfrac{dt}{dx} = \dfrac{\dfrac{x}{3}}{\sqrt{5^2 + x^2}} - \dfrac{1}{5}\)
If \(t\) has a minimum value, it happens at \(x\) such that \(\dfrac{dt}{dx} = 0\).
\(\dfrac{\dfrac{x}{3}}{\sqrt{5^2 + x^2}} - \dfrac{1}{5} = 0\)
Solve the above for \(x\). Rewrite the equation as follows.
\(5x = 3\sqrt{5^2 + x^2}\)
Square both sides.
\(25x^2 = 9(5^2 + x^2)\)
Group like terms and simplify
\(16x^2 = 225\)
Solve for \(x\) (\(x >0 \))
\(x = \sqrt{\dfrac{225}{16}} = 3.75 \, \text{km}.\)
\(\dfrac{dt}{dx}\) has one zero. The table of sign of the first derivative \(\dfrac{dt}{dx}\) is shown below.
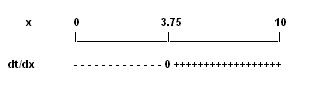
The first derivative \(\dfrac{dt}{dx}\) is negative for \(x < 3.75\), equal to zero at \(x = 3.75\) and positive for \(x > 3.75\). Also the values of \(t\) at \(x = 0\) and \(x = 10\) (the endpoints of the domain of \(t\)) are respectively \(3.6 \, \text{hrs}\) and \(3.7 \, \text{hrs}\). The value of \(t\) at \(x = 3.75\) is equal to \(3.3 \, \text{hrs}\) and it is the smallest. The answer to our problem is that one has to walk to point \(P\) such \(BP = 3.75 \, \text{km}\) then proceed along the road to \(C\) in order to get there in the shortest possible time.
Exercises
1 - Solve the same problem as above but with the following values.
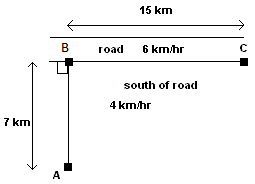
solution to the above exercise
\(x = 6.26 \, \text{km}\) (rounded to 2 decimal places).
References and Links
calculus problems




