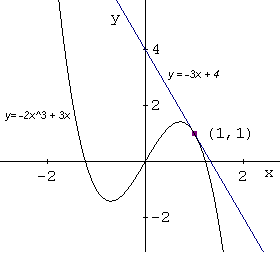Solve Tangent Lines Problems in Calculus
Tangent lines problems and their solutions, using first derivatives, are presented.
Problem 1
Find all points on the graph of \( y = x^3 - 3 x \) where the tangent line is parallel to the x axis (or horizontal tangent line).
Solution to Problem 1:
Lines that are parallel to the x axis have slope = 0. The slope of a tangent line to the graph of \( y = x^3 - 3 x \) is given by the first derivative \( y '\).
\( y ' = 3 x^2 - 3 \)
We now find all values of \( x \) for which \( y ' = 0\).
\( 3 x^2 - 3 = 0\)
Solve the above equation for \( x \) to obtain the solutions.
\( x = - 1 \) and \( x = 1\)
The above values of x are the x coordinates of the points where the tangent lines are parallel to the x axis. Find the y coordinates of these points using \( y = x^3 - 3 x \).
for \( x = - 1 \) , \( y = 2\)
for \( x = 1 \) , \( y = - 2\)
The points at which the tangent lines are parallel to the x axis are: \( (-1 , 2) \) and \( (1 , -2) \). See the graph of \( y = x^3 - 3 x \) below with the tangent lines.

Problem 2
Find the constants \( a \) and \( b \) so that the line \( y = - 3 x + 4 \) is tangent to the graph of \( y = a x^3 + b x \) at \( x = 1\).
Solution to Problem 2:
In order to find \( a \) and \( b \), we need to determine two algebraic equations in \( a \) and \( b \). The point of tangency is on the graph of \( y = a x^3 + b x \) and on the graph of \( y = - 3 x + 4\) at \( x = 1 \). Hence the y-coordinates of \( y = a x^3 + b x \) and
\( y = - 3 x + 4\) at \( x = 1 \) are equal which after substitution of \( x = 1 \) gives the equation
\( a \; (1)^3 + b \; (1) = - 3(1) + 4 \)
Simplify the above equation in \( a \) and \( b \) to obtain
\( a + b = 1 \)
The slope of the tangent line is equal to \( -3 \) which is also equal to the first derivative \( y '\) of \( y = a x^3 + b x \) at \( x = 1\)
\( y ' = 3 a x^2 + x = - 3 \) at \( x = 1 \).
Substitute \( x = 1 \) in \( 3 a x^2 + x = - 3 \) to obtain a second equation in \( a \) and \( b \)
\( 3 a + b = -3 \)
Use any method to solve the system of equations \( a + b = 1 \) and \( 3 a + b = - 3 \) obtained above to get the solution:
\( a = - 2 \) and \( b = 3 \).
See graphs of \( y = a x^3 + b x \), with \( a = - 2\) and \( b = 3 \), and \( y = - 3 x + 4 \) below.
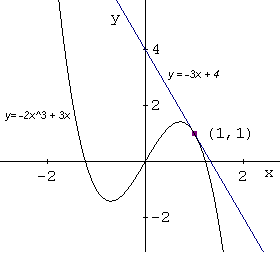
Problem 3
Find conditions on \( a \) and \( b \) so that the graph of \( y = a \; e^x + b \; x \) has NO tangent line parallel to the x axis (horizontal tangent).
Solution to Problem 3:
The slope of a tangent line is given by the first derivative \( y ' \) of \( y = a \; e^x + b \; x \). Hence
\( y ' = a \; e^x + b \)
To find the x coordinate of a point at which the tangent line to the graph of \( y\) is horizontal, solve \(y ' = 0 \) for x (slope of a horizontal line is equal to zero)
\( a e^x + b = 0 \)
Rewrite the above equation as follows
\( e^x = - b/a \)
The above equation has solutions for \( -a / b \gt 0 \). Hence, the graph of \( y = a \; e^x + b \; x \) has NO horizontal tangent line if \( - a/b \le 0 \)
Exercises
1) Find all points on the graph of \( y = x^3 - 3 x \) where the tangent line is parallel to the line whose equation is given by \( y = 9 x + 4 \).
2) Find \( a \) and \( b \) so that the line \( y = - 2 \) is tangent to the graph of \( y = a x^2 + b x \) at \( x = 1\).
3) Find conditions on \( a \), \( b \) and \( c \) so that the graph of \( y = a \; x^3 + b \; x^2 + c \; x \) has ONLY ONE tangent line parallel to the x axis (horizontal tangent line).
Solutions to the Above Exercises
1) \( (2 , 2) \) and \( (-2 , -2) \)
2) \( a = 2 \) and \( b = - 4 \)
3) \( 4 b^2 - 12 \; a \; c = 0 \)
References and Links
calculus problems