Real Life Optimization Problems in Calculus with Solutions
This page presents a collection of calculus optimization problems with complete step-by-step solutions. These problems require using derivatives to find the absolute maximum and absolute minimum of functions within a domain. Before solving these, review how to find extrema using the first and second derivatives.
General Steps for Solving Optimization Problems
- Identify the quantity to optimize (maximize or minimize).
- Draw a diagram if possible. Label knowns and unknowns.
- Write a function or formula that represents the quantity to be optimized.
- Reduce the number of variables in the function to one, using known relationships.
- Find critical points by setting the first derivative equal to zero or undefined.
- Test critical points and endpoints within the domain to determine extrema. Use the second derivative or sign analysis to confirm if extrema are minima or maxima.
Optimization Problem Examples
Problem 1: Minimum Sum with a Fixed Product
Find two positive numbers such that their product is equal to 10 and their sum is as small as possible. Verify your answer graphically.
Solution to Problem 1
Let \( x \) be the first number and \( y \) be the second number, where both \( x > 0 \) and \( y > 0 \). Let \( S \) represent the sum to be minimized.
- Sum: \( S = x + y \) ← This is the function to minimize
- Product constraint: \( x \cdot y = 10 \) ← Relationship between variables
From the constraint, solve for \( y \):
\( y = \dfrac{10}{x} \)
Substitute into the sum function to get a function of one variable:
\[
S(x) = x + \dfrac{10}{x} = \dfrac{x^2 + 10}{x}
\quad \text{with domain} \quad x > 0
\]
Optimization function in one variable
Find the first derivative of \( S(x) \):
\[
S'(x) = \dfrac{d}{dx}\left(x + \dfrac{10}{x}\right) = 1 - \dfrac{10}{x^2}
\]
Set the derivative equal to zero to find critical points:
\[
1 - \dfrac{10}{x^2} = 0 \quad \Rightarrow \quad x^2 = 10 \quad \Rightarrow \quad x = \sqrt{10}
\]
We discard \( x = -\sqrt{10} \) because \( x \) must be positive. So \( x = \sqrt{10} \) is a critical point.
Check the second derivative to determine concavity:
\[
S''(x) = \dfrac{20}{x^3}
\]
Since \( x > 0 \), \( S''(x) > 0 \), so the graph is concave up. Therefore, \( x = \sqrt{10} \) is a minimum.
The two numbers are:
\[
x = \sqrt{10} \approx 3.16, \quad y = \dfrac{10}{\sqrt{10}} = \sqrt{10} \approx 3.16
\]
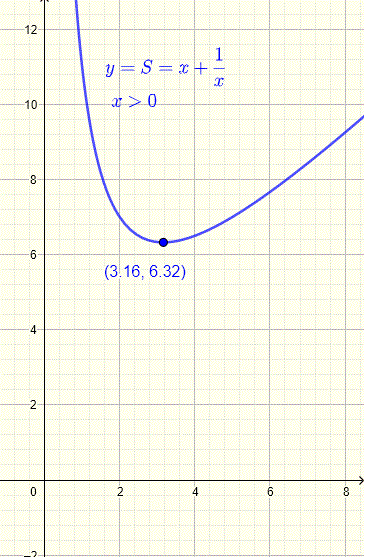
The graph of \( S(x) = x + \dfrac{10}{x} \) shows a minimum value at \( x \approx 3.16 \), confirming the result.
Problem 2: Maximize the Product of Two Numbers Given a Linear Constraint
Find two positive numbers such that the sum of six times the first and twice the second is equal to 150, and their product is as large as possible.
Solution to Problem 2
Let \( x \) be the first number and \( y \) the second number. Let \( P \) represent the product to be maximized.
The objective function is:
\[
P = x \cdot y
\]
The constraint is:
\[
6x + 2y = 150
\]
Solve the constraint for \( y \):
\[
y = 75 - 3x
\]
Substitute into the product function:
\[
P(x) = x(75 - 3x) = 75x - 3x^2
\]
Compute the first derivative:
\[
P'(x) = 75 - 6x
\]
Set the derivative equal to zero to find critical points:
\[
75 - 6x = 0 \Rightarrow x = \dfrac{75}{6} = \dfrac{25}{2}
\]
Calculate the second derivative to determine concavity:
\[
P''(x) = -6
\]
Since \( P''(x) < 0 \), the function is concave downward, confirming that \( x = \dfrac{25}{2} \) gives a maximum.
Now find \( y \):
\[
y = 75 - 3x = 75 - 3 \cdot \dfrac{25}{2} = \dfrac{75}{2}
\]
Conclusion: The two positive numbers that maximize the product under the constraint are:
- \( x = \dfrac{25}{2} = 12.5 \)
- \( y = \dfrac{75}{2} = 37.5 \)
Problem 3: Maximize the Area of Two Rectangles
Suppose you have to fence two rectangular fields with the same dimensions, with one side in common, using 180 meters of fencing. Find the dimensions of the rectangles so that the total fenced area is maximum.
Solution to Problem 3
Let \( L \) be the length and \( W \) the width of each rectangle. The width is the shared side.

Total area: \( A = 2LW \)
Fencing constraint: \( 4L + 3W = 180 \).
Solve for \( W \): \( W = 60 - \dfrac{4}{3}L \).
Area as a function of \( L \):
\[ A(L) = 2L \left(60 - \dfrac{4}{3}L \right) = -\dfrac{8}{3}L^2 + 120L \]
From the graph of \( 4L + 3W = 180 \), the domain is \( L \in [0, 45] \).
Derivative: \( A'(L) = -\dfrac{16}{3}L + 120 \).
Solve \( A'(L) = 0 \Rightarrow L = 22.5 \).
Evaluate:
- \( A(0) = 0 \)
- \( A(45) = 0 \)
- \( A(22.5) = -\dfrac{8}{3}(22.5)^2 + 120 \cdot 22.5 = 1350 \)
Maximum area occurs at \( L = 22.5 \), \( W = 60 - \dfrac{4}{3} \cdot 22.5 = 30 \).
Dimensions: \( 22.5 \) m by \( 30 \) m.
Problem 4: Minimize Area of a Square and Circle from 100 cm Wire
A wire of length 100 cm is cut into two pieces. One piece is bent to form a square, and the other is bent to form a circle. Find the lengths of the two pieces so that the sum of the areas enclosed by the square and the circle is minimized.
Solution to Problem 4
Let:
- \( x \): length of wire used for the square
- \( y \): length of wire used for the circle
Since the total wire is 100 cm, we have:
\[
x + y = 100
\]
Let \( A \) be the total enclosed area.
Step 1: Express Areas in Terms of \( x \)
For the square:
\[
x = 4s \Rightarrow s = \dfrac{x}{4}
\]
\[
A_{\text{square}} = s^2 = \left(\dfrac{x}{4}\right)^2 = \dfrac{x^2}{16}
\]
For the circle:
\[
y = 2\pi r \Rightarrow r = \dfrac{y}{2\pi}
\]
\[
A_{\text{circle}} = \pi r^2 = \pi \left( \dfrac{y}{2\pi} \right)^2 = \dfrac{y^2}{4\pi}
\]
Total area:
\[
A(x) = \dfrac{x^2}{16} + \dfrac{(100 - x)^2}{4\pi}
\]
Step 2: Minimize the Area
Take the derivative:
\[
A'(x) = \dfrac{x}{8} - \dfrac{1}{2\pi}(100 - x)
\]
Set derivative equal to 0:
\[
\dfrac{x}{8} = \dfrac{1}{2\pi}(100 - x)
\]
Multiply both sides by \( 8 \cdot 2\pi \):
\[
2\pi x = 8(100 - x)
\]
\[
2\pi x + 8x = 800 \Rightarrow x(2\pi + 8) = 800
\Rightarrow x = \dfrac{800}{2\pi + 8} = \dfrac{400}{\pi + 4}
\]
Approximating:
\[
x \approx \dfrac{400}{7.14} \approx 56 \text{ cm}
\]
\[
y = 100 - x \approx 44 \text{ cm}
\]
Step 3: Verify Minimum
Evaluate the area at endpoints and the critical point:
\[
A(0) = \dfrac{0^2}{16} + \dfrac{100^2}{4\pi} \approx 795
\]
\[
A(100) = \dfrac{100^2}{16} + \dfrac{0^2}{4\pi} = 625
\]
\[
A(56) \approx \dfrac{56^2}{16} + \dfrac{(44)^2}{4\pi} \approx 350
\]
Final Answer
- Use approximately 56 cm of wire for the square
- Use approximately 44 cm of wire for the circle
- This configuration minimizes the total enclosed area
Problem 5 – Maximum Volume of a Box with Square Ends
A box with square ends of side \( x \) and a length \( L \) is to be made such that \( L + 4x = 4 \) meters.
Find the dimensions of the box that maximize its volume.
Solution to Problem 5
The area of a square end is \( x^2 \).
The volume \( V \) of the box is:
\[ V = x^2 L \]
From the constraint \( L + 4x = 4 \), solve for \( L \):
\[ L = 4 - 4x \]
Substitute into the expression for volume:
\[ V(x) = x^2(4 - 4x) \]
To determine the domain of \( V(x) \):
The smallest value of \( x \) is \( 0 \). The largest value occurs when \( L = 0 \), which gives \( x = 1 \).
So, the domain is \( x \in [0, 1] \).
Differentiate \( V(x) \):
\[ V'(x) = 8x - 12x^2 \]
Find the critical points by solving:
\[ 8x - 12x^2 = 0 \quad \Rightarrow \quad x(8 - 12x) = 0 \quad \Rightarrow \quad x = 0 \text{ or } x = \dfrac{2}{3} \]
Evaluate the volume at the endpoints and critical point:
- \( V(0) = 0^2(4 - 0) = 0 \)
- \( V\left(\dfrac{2}{3}\right) = \left(\dfrac{2}{3}\right)^2 \left(4 - \dfrac{8}{3}\right) = \dfrac{4}{9} \cdot \dfrac{4}{3} = \dfrac{16}{27} \)
- \( V(1) = 1^2(4 - 4) = 0 \)
The volume is maximized at \( x = \dfrac{2}{3} \) meters.
Now substitute \( x = \dfrac{2}{3} \) into the constraint to find \( L \):
\[ L = 4 - 4 \cdot \dfrac{2}{3} = \dfrac{4}{3} \text{ meters} \]
Final Answer:
The box has square ends of side \( \dfrac{2}{3} \) meters and length \( \dfrac{4}{3} \) meters, which gives the maximum volume of \( \dfrac{16}{27} \text{ m}^3 \).
Problem 6: Maximizing Profit for Selling Electronic Calculators
The total cost, including manufacture, packaging, and distribution, of an electronic calculator is
$21. If the machine sells at a price of
\( x \) dollars each, the number \( n \) of machines sold is given by:
\[
n(x) = \dfrac{200}{x - 21} + 10(50 - x)
\]
Solution to Problem 6
Let \( R_t \) be the total revenue from selling \( n \) calculators:
\[
R_t = n \cdot x
\]
Let \( C_t \) be the total cost of manufacturing, packaging, and distribution:
\[
C_t = 21 \cdot n
\]
Then, the profit function is:
\[
P(x) = R_t - C_t = n(x - 21)
\]
Substitute the expression for \( n \):
\[
P(x) = \left( \dfrac{200}{x - 21} + 10(50 - x) \right)(x - 21)
\]
Simplify:
\[
P(x) = 200 + 10(50 - x)(x - 21)
\]
\[
P(x) = -10x^2 + 710x - 10300
\]
Domain of the profit function:
Since the selling price must be greater than the cost price, we take
\[
x > 21
\]
and there is no strict upper bound, so the domain is
\[
x \in (21, \infty)
\]
Step 1: Find Critical Points
Differentiate \( P(x) \) with respect to \( x \):
\[
P'(x) = -20x + 710
\]
Set the derivative equal to zero:
\[
-20x + 710 = 0 \quad \Rightarrow \quad x = 35.5
\]
Step 2: Confirm Maximum
Find the second derivative:
\[
P''(x) = -20
\]
Since \( P''(x) \lt 0 \), the graph is concave down, confirming that the profit has a maximum at:
\[
x = 35.5
\]
Final Answer
The selling price that maximizes the profit is:
\[
\boxed{x = 35.5 \text{ dollars}}
\]
Problem 7: Largest Rectangle Under the Curve \( y = \dfrac{1}{x²+1} \)
We want to find the dimensions of the rectangle with the largest area that can be inscribed under the curve
\[
y = \dfrac{1}{x^2 + 1}
\]
and above the x-axis.
Solution to Problem 7
Let \(x\) be half the base length of the rectangle. The top-right vertex of the rectangle lies on the curve, so its y-coordinate is
\[
y = \dfrac{1}{x^2 + 1}.
\]

The area of the rectangle is therefore:
\[
A(x) = 2x \cdot \dfrac{1}{x^2 + 1}.
\]
The domain of \(A(x)\) is:
\[
x \in [0, \infty).
\]
Differentiate \(A(x)\):
\[
A'(x) = \dfrac{2(x^2 + 1) - 4x^2}{(x^2+1)^2}
= \dfrac{2(1 - x^2)}{(x^2+1)^2}.
\]
Set derivative equal to zero:
\[
1 - x^2 = 0 \quad \Rightarrow \quad x = \pm 1.
\]
Since \(x \geq 0\), we take \(x = 1\).
Compute the second derivative:
\[
A''(x) = -\dfrac{4x(-x^2+3)}{(x^2+1)^3}.
\]
At \(x = 1\):
\[
A''(1) = -1 \lt 0,
\]
so the function is concave down, confirming a maximum.
Final Answer
The rectangle with the largest area has dimensions:
\[
\text{Length} = 2x = 2(1) = 2,
\quad
\text{Width} = \dfrac{1}{1^2+1} = \dfrac{1}{2}.
\]
Thus, the maximum-area rectangle measures 2 units by 0.5 units.
Problem 8: Largest Rectangle Inscribed in a Right Triangle with Height 4 and Hypotenuse 5
Find the dimensions of the rectangle with the largest area that can be inscribed in a right triangle with height 4 and hypotenuse 5.
Solution to Problem 8
A diagram is helpful to visualize the problem.

Let the rectangle have width \( w \) and height \( h \). Its area is
\[
A = h \cdot w.
\]
Using the Pythagorean theorem, the base \( BC \) of the right triangle is
\[
BC = \sqrt{5^2 - 4^2} = 3.
\]
Triangles \( AEF \) and \( ABC \) are similar, so the ratios of corresponding sides satisfy
\[
\dfrac{AE}{EF} = \dfrac{AB}{BC}.
\]
Here,
\[
AE = 4 - h, \quad EF = w, \quad AB = 4, \quad BC = 3.
\]
Substituting, we get
\[
\dfrac{4 - h}{w} = \dfrac{4}{3} \implies h = -\dfrac{4}{3} w + 4.
\]
Substitute \( h \) into the area formula:
\[
A(w) = \left(-\dfrac{4}{3} w + 4\right) w = -\dfrac{4}{3} w^2 + 4w.
\]
The domain of \( A \) is
\[
w \in [0, 3].
\]
Compute the first derivative of \( A \):
\[
A'(w) = -\dfrac{8}{3} w + 4.
\]
Set derivative to zero to find critical points:
\[
-\dfrac{8}{3} w + 4 = 0 \implies w = \dfrac{3}{2} = 1.5.
\]
Evaluate the area at the critical point and endpoints:
\[
A\left(\dfrac{3}{2}\right) = 3, \quad A(0) = 0, \quad A(3) = 0.
\]
Final Answer
The rectangle with the largest area has dimensions:
\[
w = \dfrac{3}{2} = 1.5,
\quad
h = -\dfrac{4}{3} \times \dfrac{3}{2} + 4 = 2.
\]
Problem 9: Show Analytically that \( f(x) = -5 - 4 \cos(x) + \cos(2x) \) is Never Positive on \( [0, 2\pi] \)
Show analytically that the function
\[
f(x) = -5 - 4 \cos(x) + \cos(2x), \quad \text{for} \quad 0 \leq x \leq 2\pi,
\]
is never positive.
Solution to Problem 9
To prove that \( f(x) \) is never positive, we show that its maximum value on \( [0, 2\pi] \) is less than or equal to zero.
Calculate the first derivative:
\[
f'(x) = 4 \sin(x) - 2 \sin(2x).
\]
Using the identity \( \sin(2x) = 2 \sin(x) \cos(x) \), rewrite:
\[
f'(x) = 4 \sin(x) - 4 \sin(x) \cos(x) = 4 \sin(x) (1 - \cos(x)).
\]
Set the derivative equal to zero to find critical points:
\[
4 \sin(x) (1 - \cos(x)) = 0.
\]
This implies
\[
\sin(x) = 0 \quad \text{or} \quad \cos(x) = 1.
\]
Solutions within \( [0, 2\pi] \) are:
\[
\sin(x) = 0 \implies x = 0, \pi, 2\pi,
\]
\[
\cos(x) = 1 \implies x = 0, 2\pi.
\]
Evaluate \( f(x) \) at these points:
\[
f(0) = -5 - 4 \cos(0) + \cos(0) = -5 - 4(1) + 1 = -8,
\]
\[
f(2\pi) = -5 - 4 \cos(2\pi) + \cos(4\pi) = -5 - 4(1) + 1 = -8,
\]
\[
f(\pi) = -5 - 4 \cos(\pi) + \cos(2\pi) = -5 - 4(-1) + 1 = 0.
\]
Conclusion
Since the maximum value of \( f(x) \) on \( [0, 2\pi] \) is \( 0 \), the function \( f(x) \) is never positive on the interval.
Problem 10: Maximize the Volume of a Cone with Fixed Slant Height
Find the radius \( r \) of the base of a cone and its altitude \( h \) such that the slant height is \( 5 \) cm and the volume is maximum.
Solution to Problem 10
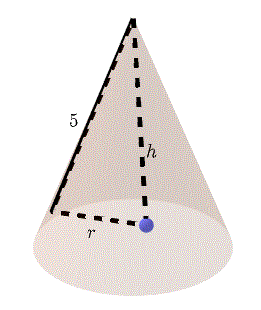 The volume of a cone with radius \( r \) and altitude \( h \) is
\[
V = \dfrac{1}{3} \pi r^2 h.
\]
Using the Pythagorean theorem for the slant height,
\[
h^2 + r^2 = 5^2 = 25,
\]
so
\[
h = \sqrt{25 - r^2}.
\]
Substitute \( h \) into the volume formula:
\[
V(r) = \dfrac{1}{3} \pi r^2 \sqrt{25 - r^2}.
\]
The domain is
\[
r \in [0, 5].
\]
The volume of a cone with radius \( r \) and altitude \( h \) is
\[
V = \dfrac{1}{3} \pi r^2 h.
\]
Using the Pythagorean theorem for the slant height,
\[
h^2 + r^2 = 5^2 = 25,
\]
so
\[
h = \sqrt{25 - r^2}.
\]
Substitute \( h \) into the volume formula:
\[
V(r) = \dfrac{1}{3} \pi r^2 \sqrt{25 - r^2}.
\]
The domain is
\[
r \in [0, 5].
\]
Calculate the first derivative \( V'(r) \):
\[
V'(r) = \dfrac{\pi}{3} \left( 2r \sqrt{25 - r^2} + r^2 \cdot \dfrac{1}{2} \cdot (-2r) (25 - r^2)^{-1/2} \right) = \dfrac{\pi}{3} \dfrac{50r - 3r^3}{\sqrt{25 - r^2}}.
\]
Set the numerator equal to zero to find critical points:
\[
50 r - 3 r^3 = 0 \implies r (50 - 3 r^2) = 0.
\]
Critical points are
\[
r = 0, \quad r = \sqrt{\dfrac{50}{3}} \approx 4.08, \quad r = -\sqrt{\dfrac{50}{3}} \approx -4.08.
\]
Exclude \( r = -4.08 \) since it is not in the domain.
Note that \( r = 5 \) makes the denominator zero, so \( V'(r) \) is undefined there but still consider \( r = 5 \) as endpoint.
Evaluate \( V \) at critical points and endpoints:
\[
V\left(\sqrt{\dfrac{50}{3}}\right) = \dfrac{1}{3} \pi \left(\sqrt{\dfrac{50}{3}}\right)^2 \sqrt{25 - \left(\sqrt{\dfrac{50}{3}}\right)^2} \approx 50.38,
\]
\[
V(0) = 0, \quad V(5) = 0.
\]
Therefore, the volume is maximized at
\[
r = \sqrt{\dfrac{50}{3}} \approx 4.08.
\]
Calculate the corresponding altitude:
\[
h = \sqrt{25 - r^2} = \sqrt{25 - \dfrac{50}{3}} = \dfrac{5}{\sqrt{3}} \approx 2.88.
\]
Problem 11: Find the Point on a Line Closest to a Given Point
Find the point on the line defined by
\[
y = 4 - x
\]
that is closest to the point \( (6, 3) \).
Solution to Problem 11
Any point \( M \) on the line can be written as
\[
M = (x, 4 - x).
\]
The distance \( D \) between \( M \) and the point \( (6, 3) \) is
\[
D = \sqrt{(x - 6)^2 + (4 - x - 3)^2} = \sqrt{(x - 6)^2 + (1 - x)^2}.
\]
The domain of \( D \) is
\[
x \in (-\infty, \infty).
\]
We seek the \( x \) that minimizes \( D \).
Calculate the first derivative of \( D \):
\[
D' = \dfrac{1}{2} \dfrac{4x - 14}{\sqrt{2x^2 - 14x + 37}}.
\]
Set the numerator equal to zero to find critical points:
\[
4x - 14 = 0 \implies x = \dfrac{7}{2}.
\]
Since the denominator is always positive, the sign of \( D' \) depends on the numerator:
- For \( x < \dfrac{7}{2} \), \( D' < 0 \) (distance decreasing),
- For \( x > \dfrac{7}{2} \), \( D' > 0 \) (distance increasing).
Hence, \( D \) has a minimum at
\[
x = \dfrac{7}{2}.
\]
Find the corresponding \( y \) coordinate:
\[
y = 4 - x = 4 - \dfrac{7}{2} = \dfrac{1}{2}.
\]
Therefore, the point on the line closest to \( (6, 3) \) is
\[
\boxed{\left( \dfrac{7}{2}, \dfrac{1}{2} \right)}.
\]

Problem 12: Minimize the Total Cost of Building a Pipeline Offshore and Along the Coast
A company plans to build a pipeline from point \( A \) offshore (in the ocean) to point \( B \) along the coastline. The cost of building the pipeline along the coastline is \( k \) dollars per kilometer, and the cost offshore is \( 3k \) dollars per kilometer, where \( k \) is a constant. Find the distances of the pipeline offshore from \( A \) to \( D \) and along the coast from \( D \) to \( B \) that minimize the total cost of the pipeline.

Solution to Problem 12
Let \( x \) be the distance from \( D \) to \( B \) along the coastline, and \( y \) be the offshore distance from \( A \) to \( D \).
Using the Pythagorean theorem in triangle \( ACB \), we find the length \( CB \):
\[
CB = \sqrt{50^2 - 30^2} = 40 \text{ km}.
\]
The length \( CD \) along the coast is
\[
CD = CB - x = 40 - x.
\]
Using the Pythagorean theorem in triangle \( ACD \):
\[
y = \sqrt{30^2 + (40 - x)^2}.
\]
The total cost \( C_t \) of the pipeline is
\[
C_t(x) = k x + 3 k y = k x + 3 k \sqrt{30^2 + (40 - x)^2}.
\]
The domain for \( x \) is
\[
x \in [0, 40].
\]
Calculate the derivative of \( C_t \):
\[
C_t'(x) = k - 3k \cdot \dfrac{40 - x}{\sqrt{30^2 + (40 - x)^2}} = k \cdot \dfrac{\sqrt{30^2 + (40 - x)^2} - 3(40 - x)}{\sqrt{30^2 + (40 - x)^2}}.
\]
Set the numerator equal to zero to find critical points:
\[
\sqrt{30^2 + (40 - x)^2} = 3(40 - x).
\]
Square both sides:
\[
30^2 + (40 - x)^2 = 9(40 - x)^2.
\]
Simplify:
\[
30^2 + (40 - x)^2 = 9(40 - x)^2 \implies 30^2 = 8(40 - x)^2.
\]
Rearranging gives the quadratic equation
\[
-8x^2 + 640x - 11900 = 0.
\]
Solving the quadratic, the valid solution in the domain is
\[
x = \dfrac{80 - 15 \sqrt{2}}{2} \approx 29.40 \text{ km}.
\]
Evaluate the total cost at the endpoints and critical point:
\[
C_t(0) = 150 k, \quad C_t(40) = 130 k, \quad C_t(29.40) \approx 124.85 k.
\]
Thus, the minimum cost occurs at \( x \approx 29.40 \) km.
Find the offshore distance \( y \):
\[
y = \sqrt{30^2 + (40 - 29.40)^2} \approx 31.81 \text{ km}.
\]
Problem 13: Prove the Maximum Product under the Constraint \( x + y = K \)
Show that if \( x + y = K \), where \( K \) is a constant, then
\[
x \cdot y \le \left(\dfrac{K}{2}\right)^2.
\]
Here, \( x \), \( y \), and \( K \) are real numbers.
Solution to Problem 13
We want to show that the product \( x \cdot y \) has a maximum value less than or equal to \( \left(\dfrac{K}{2}\right)^2 \).
Express \( y \) in terms of \( x \):
\[
y = K - x.
\]
Define the product function:
\[
P(x) = x \cdot y = x(K - x) = -x^2 + Kx.
\]
The domain of \( P \) is
\[
x \in (-\infty, \infty).
\]
Calculate the first derivative of \( P \) (with \( K \) constant):
\[
P'(x) = -2x + K.
\]
Find the critical points by solving \( P'(x) = 0 \):
\[
-2x + K = 0 \implies x = \dfrac{K}{2}.
\]
Calculate the second derivative:
\[
P''(x) = -2.
\]
Since \( P''(x) \lt 0 \), \( P \) is concave down and therefore has a maximum at \( x = \dfrac{K}{2} \).
Find the corresponding \( y \):
\[
y = K - x = K - \dfrac{K}{2} = \dfrac{K}{2}.
\]
Evaluate the maximum product:
\[
P\left(\dfrac{K}{2}\right) = \dfrac{K}{2} \cdot \dfrac{K}{2} = \left(\dfrac{K}{2}\right)^2.
\]
Hence,
\[
x \cdot y \le \left(\dfrac{K}{2}\right)^2.
\]
More References and Links
- Absolute Minimum and Maximum of a Function.
-
Calculus Questions, Answers and Solutions.
-
Free Calculus Tutorials and Problems.




 The volume of a cone with radius \( r \) and altitude \( h \) is
\[
V = \dfrac{1}{3} \pi r^2 h.
\]
Using the Pythagorean theorem for the slant height,
\[
h^2 + r^2 = 5^2 = 25,
\]
so
\[
h = \sqrt{25 - r^2}.
\]
Substitute \( h \) into the volume formula:
\[
V(r) = \dfrac{1}{3} \pi r^2 \sqrt{25 - r^2}.
\]
The domain is
\[
r \in [0, 5].
\]
The volume of a cone with radius \( r \) and altitude \( h \) is
\[
V = \dfrac{1}{3} \pi r^2 h.
\]
Using the Pythagorean theorem for the slant height,
\[
h^2 + r^2 = 5^2 = 25,
\]
so
\[
h = \sqrt{25 - r^2}.
\]
Substitute \( h \) into the volume formula:
\[
V(r) = \dfrac{1}{3} \pi r^2 \sqrt{25 - r^2}.
\]
The domain is
\[
r \in [0, 5].
\]

