Continuous Functions in Calculus
We present an introduction and the definition of the concept of continuous functions in calculus with examples. Also continuity theorems and their use in calculus are also discussed.
Introduction and Definition of Continuous Functions
We first start with graphs of several continuous functions. The functions whose graphs are shown below are said to be continuous since these graphs have no "breaks", "gaps" or "holes".

We now present examples of discontinuous functions. These graphs have: breaks, gaps or points at which they are undefined.
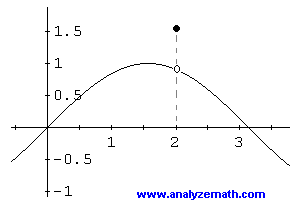
In the graphs below, the function is undefined at \( x = 2 \). The graph has a hole at \( x = 2 \) and the function is said to be discontinuous.

In the graphs below, the limits of the function to the left and to the right are not equal and therefore the limit at \( x = 3 \) does not exist. The function is said to be discontinuous.

The limits of the function at \( x = 2 \) exist but it is not equal to the value of the function at \( x = 2 \). This function is also discontinuous.
The limits of the function at \( x = 3 \) does does not exist since to the left and to the right of 3 the function either increases or decreases indefinitely. This function is also discontinuous.

Taking into consideration all the information gathered from the examples of continuous and discontinuous functions shown above, we define a continuous functions as follows:
Function \( f \) is continuous at a point \( a \) if the following conditions are satisfied.
1. \(\lim_{x\to a} f(x)\) is defined
2. \(\lim_{x\to a} f(x)\) exists
3. \(\lim_{x\to a} f(x) = f(a)\)
Examples with Solutions
Example 1
Show that function \( f \) defined below is not continuous at \( x = - 2 \).
\( f(x) = \dfrac{1}{x + 2} \)
Solution to Example 1
\( f(-2) \) is undefined (division by 0 not allowed) therefore function \( f \) is discontinuous at \( x = - 2 \).
Example 2
Show that function \( f \) is continuous for all values of \( x \) in \( \mathbb{R} \).
\( f(x) = \dfrac{1}{x^4 + 6} \)
Solution to Example 2
Function \( f \) is defined for all values of \( x \) in \( \mathbb{R} \). The limit of \( f \) at say \( x = a \) is given by the quotient of two limits: the constant 1 and the limit of \( x^4 + 6 \) which is a polynomial function and its limit is \( a^4 + 6 \). Hence
\(\lim_{x\to a} f(x) = \dfrac{1}{a^4+6}\)
\( f(a) = \dfrac{1}{a^4 + 6} \). Hence
\(\lim_{x\to a} f(x) = f(a)\)
The three conditions of continuity are satisfied and therefore \( f \) is continuous for all values of \( x \) in \( \mathbb{R} \).
Example 3
Show that function \( f \) is continuous for all values of \( x \) in \( \mathbb{R} \).
\( f(x) = | x - 5 | \)
Solution to Example 3
Let us first write \( f(x) \) as follows. Hence
\( f(x) = x - 5 \) if \( x > 5 \)
\( f(x) = -(x - 5) \) if \( x \lt 5 \)
\( f(x) = 0 \) if \( x = 5 \)
\( f(x) \) is given by the polynomial functions \( x - 5 \) and \(-(x - 5) \) if \( x > 5 \) and \( x \lt 5 \) respectively and hence \( f(x) \) is continuous for these values of \( x \).
\( x = 5 \) is the only value of \( x \) to be considered. We now consider the limits of \( f \) as \( x \) approaches \( 5 \) from the left (\( x \lt 5 \)) when \( f(x) = -(x - 5) \).
\(\lim_{x\to 5^{-}} f(x) = \lim_{x\to 5^{-}} - (x - 5) = 0\)
We now consider the limits of \( f \) as \( x \) approaches \( 5 \) from the right (\( x > 5 \)) when
\( f(x) = (x - 5) \).
\(\lim_{x\to 5^{+}} f(x) = \lim_{x\to 5^{+}} (x - 5) = 0\)
Since the two limits are equal the limit \( \lim_{x\to 5} f(x) \) exists and is equal to 0. Hence \( \lim_{x\to 5} f(x) = 0 = f(5) \) and function \( f \) is continuous at \( x = 5 \). Taking into consideration what was said above for \( x > 5 \) and \( \lt 5 \), \( f \) is continuous for all values of \( x \) in \( \mathbb{R} \).
More references and Links
Calculus Tutorials and Problems





