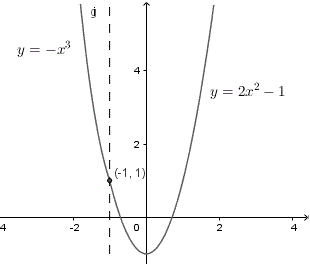
Questions with answers on the continuity of functions with emphasis on rational and piecewise functions. The continuity of a function and its derivative at a given point is discussed. Graphical meaning and interpretation of continuity are also included.
Solution to Example 1
a) For \( x = 0 \), the denominator of function \( f(x) \) is equal to \( 0 \) and \( f(x) \) is not defined and does not have a limit at \( x = 0 \). Therefore function \( f(x) \) is discontinuous at \( x = 0 \).
b) For \( x = 2 \) the denominator of function \( g(x) \) is equal to 0 and function \( g(x) \) not defined at \( x = 2 \) and it has no limit. Function \( g(x) \) is not continuous at \( x = 2 \).
c) The denominator of function \( h(x) \) can be factored as follows: \( x^2 -1 = (x - 1)(x + 1) \). The denominator is equal to 0 for \( x = 1 \) and \( x = -1 \) values for which the function is undefined and has no limits. Function \( h \) is discontinuous at \( x = 1 \) and \( x = -1 \).
d) \( \tan(x) \) is undefined for all values of \( x \) such that \( x = \frac{\pi}{2} + k \pi , \) where \( k \) is any integer (\( k = 0, -1, 1, -2, 2,...) \) and is therefore discontinuous for these same values of \( x \).
e) The denominator of function \( j(x) \) is equal to 0 for \( x \) such that \( \cos(x) - 1 = 0 \) or \( x = k (2 \pi) \), where \( k \) is any integer and therefore this function is undefined and therefore discontinuous for all these same values of \( x \).
f) Function \( k(x) \) is defined as the ratio of two continuous functions (with denominator \( x^2 + 5 \) never equal to 0), is defined for all real values of \( x \) and therefore has no point of discontinuity.
g) \( l(x) = \dfrac{x + 4}{x + 4} = 1 \) for \( x \ne - 4 \).
\( \lim_{x \to -4} l(x) = 1 = l(-4) \).
Function \( l(x) \) is continuous for all real values of \( x \) and therefore has no point of discontinuity.
Solution to Example 2
For \( x > -1 \), \( f(x) = 2 x^ 2 + b \) is a polynomial function and therefore continuous.
For \( x \lt -1 \), \( f(x) = -x^3 \) is a polynomial function and therefore continuous.
For \( x = -1 \)
\( f(-1) = 2(-1)^ 2 + b = 2 + b \)
let us consider the left and right hand limits
\( L1 = \lim_{x\to -1^-} f(x) = -(-1)^3 = 1 \)
\( L2 = \lim_{x\to -1^+} f(x) = 2(-1)^2 + b = 2 + b \)
For function \( f \) to be continuous, we need to have
\( L2 = L1 \)
or \( 2 + b = 1 \)
Solve for \( b \)
\( b = -1 \).
Substitute \( b \) by -1 in the given function to obtain
\[ f(x) = \begin{cases}
2x^2-1 & x \ge -1 \\
-x^3 & x \lt -1 \\
\end{cases}
\]
The graph of \( f \) is shown below and it is clear that the function is continuous at \( x = -1 \).
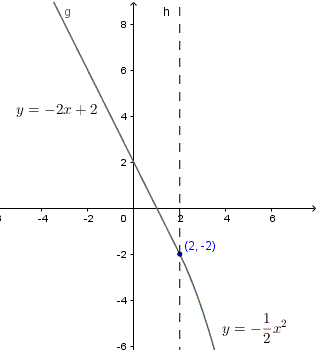
Solution to Example 3
Continuity of function \( g \)
For \( x > 2 \), \( g(x) = a x^ 2 + b \) is a polynomial function and therefore continuous.
For \( x < 2 \), \( g(x) = -2 x + 2 \) is a polynomial function and therefore continuous.
let
\( L1 = \lim_{x\to 2^+} g(x) = a (2)^2 + b = 4 a + b \)
\( L2 = \lim_{x\to 2^-} g(x) = -2(2) + 2 = -2 \)
For continuity of \( g \) at \( x = 2 \), we need to have
\( L1 = L2 = g(2) \)
Which gives
\( 4 a + b = -2 \)
Continuity of the derivative \( g' \)
For \( x > 2 \), \( g '(x) = 2 a x \) is a polynomial function and therefore continuous.
For \( x \lt 2 \), \( g '(x) = -2 \) is a constant function and therefore continuous.
Let
\( l1 = \lim_{x\to 2^+} g'(x) = 2a(2) = 4 a \)
\( l2 = \lim_{x\to 2^-} g'(x) = -2 \)
For continuity of \( g' \) at \( x = 2 \), we need to have
\( l1 = l2 \) or \( 4 a = - 2 \)
Solve the last equation to obtain: \( a = - 1 / 2 \).
Substitute \( a \) by \( - 1 / 2 \) in the equation \( 4 a + b = -2 \) obtained above and solve for \( b \) to obtain \( b = 0 \).
Substitute \( a \) and \( b \) by their values to obtain function \( g \):
\[ g(x) = \begin{cases}
-\dfrac{1}{2}x^2 & x \ge 2 \\
-2x+2 & x \lt 2 \\
\end{cases} \]
Function \( g(x) \) is graphed below and it is clear that both the function and its derivative (slope) are continuous at \( x = 2 \).