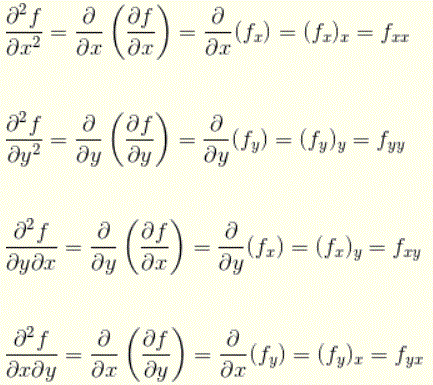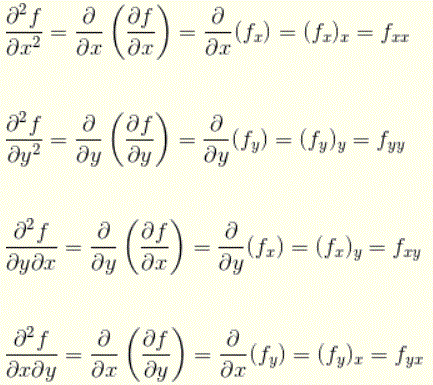Second Order Partial Derivatives in Calculus
Examples with detailed solutions on how to calculate second order partial derivatives are presented.
Definitions and Notations of Second Order Partial Derivatives
For a two variable function \( f(x , y) \), we can define 4 second order partial derivatives along with their notations.
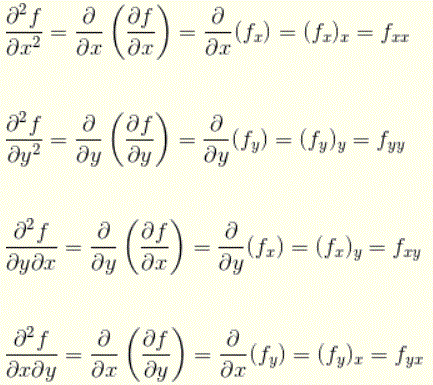
Examples with Detailed Solutions on Second Order Partial Derivatives
Example 1
Find \( f_{xx} \), \( f_{yy} \) given that \( f(x , y) = \sin(x y) \).
Solution
\( f_{xx} \) may be calculated as follows
\[
f_{xx} = \frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial}{\partial x}\left(\frac{\partial}{\partial x}\sin (x y)\right) = \frac{\partial}{\partial x}(y \cos (x y)) = - y^2 \sin (x y)
\]
\( f_{yy} \) can be calculated as follows
\[
f_{yy} = \frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial}{\partial y}\left(\frac{\partial}{\partial y}\sin (x y)\right) = \frac{\partial}{\partial y}(x \cos (x y)) = - x^2 \sin (x y)
\]
Example 2
Find \( f_{xx} \), \( f_{yy} \), \( f_{xy} \), \( f_{yx} \) given that \( f(x , y) = x^3 + 2 x y \).
Solution
\( f_{xx} \) is calculated as follows
\[
f_{xx} = \frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial}{\partial x}\left(\frac{\partial}{\partial x}(x^3 + 2 x y)\right) = \frac{\partial}{\partial x}(3 x^2 + 2 y) = 6x
\]
\( f_{yy} \) is calculated as follows
\[
f_{yy} = \frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial}{\partial y}\left(\frac{\partial}{\partial y}(x^3 + 2 x y)\right) = \frac{\partial}{\partial y}(2x) = 0
\]
\( f_{xy} \) is calculated as follows
\[
f_{xy} = \frac{\partial^2 f}{\partial y\partial x} = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial}{\partial y}\left(\frac{\partial}{\partial x}(x^3 + 2 x y)\right) = \frac{\partial}{\partial y}(3 x^2 + 2 y) = 2
\]
\( f_{yx} \) is calculated as follows
\[
f_{yx} = \frac{\partial^2 f}{\partial x\partial y} = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}(x^3 + 2 x y)\right) = \frac{\partial}{\partial x}(2x) = 2
\]
Example 3
Find \( f_{xx} \), \( f_{yy} \), \( f_{xy} \), \( f_{yx} \) given that \( f(x , y) = x^3y^4 + x^2 y \).
Solution
\( f_{xx} \) is
calculated as follows
\[
f_{xx} = \frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial}{\partial x}\left(\frac{\partial}{\partial x}(x^3y^4 + x^2 y)\right) = \frac{\partial}{\partial x}(3 x^2y^4 + 2 x y) = 6xy^4 + 2 y
\]
\( f_{yy} \) is calculated as follows
\[
f_{yy} = \frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial}{\partial y}\left(\frac{\partial}{\partial y}(x^3y^4 + x^2 y)\right) = \frac{\partial}{\partial y}(4x^3y^3 + x^2) = 12x^3y^2
\]
\( f_{xy} \) is calculated as follows
\[
f_{xy} = \frac{\partial^2 f}{\partial y\partial x} = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial}{\partial y}\left(\frac{\partial}{\partial x}(x^3y^4 + x^2 y)\right) = \frac{\partial}{\partial y}(3x^2y^4 + 2 x y) = 12x^2y^3 + 2x
\]
\( f_{yx} \) is calculated as follows
\[
f_{yx} = \frac{\partial^2 f}{\partial x\partial y} = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}(x^3y^4 + x^2 y)\right) = \frac{\partial}{\partial x}(4x^3y^3 + x^2) = 12x^2y^3 + 2x
\]
More References and Links to Partial Derivatives and Multivariable Functions
Multivariable Functions