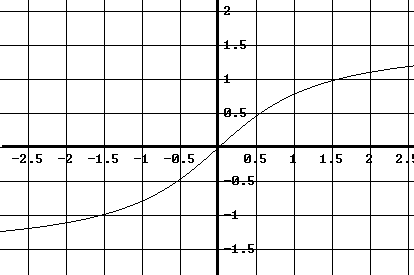Graphical Approximation of Derivatives - Part(3)

Approximate graphically the first derivative of a function \( f \) from its graph. Each question is followed by a detailed solution explaining the reasoning.

Question 1

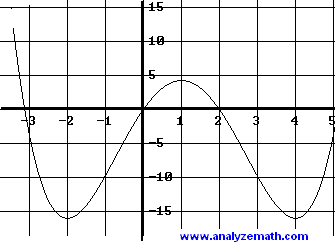
Below is shown the graph of a function \( f \).

a) Assuming that the only extrema of \( f \) are the ones shown on the graph, for which values of \( x \) is \[ f'(x) = 0 \, ? \]

b) Assuming that the graph of \( f \) rises indefinitely to the left and to the right, determine the intervals where \[ f'(x) < 0 \quad \text{and} \quad f'(x) > 0 . \]

Solution to Question 1

a) The graph of \( f \) has two local minima at \[ x = -2 \quad \text{and} \quad x = 4 \] and one local maximum at \[ x = 1 . \] Therefore, \[ f'(x) = 0 \quad \text{for} \quad x = -2,\; 1,\; 4 . \]
b) The function \( f \) is decreasing on the intervals \[ (-\infty, -2) \quad \text{and} \quad (1, 4), \] so \[ f'(x) < 0 \quad \text{on these intervals.} \]
The function \( f \) is increasing on \[ (-2, 1) \quad \text{and} \quad (4, +\infty), \] hence \[ f'(x) > 0 \quad \text{on these intervals.} \]

Question 2

The graph of a function \( f \) is shown below. Assuming that \( f \) is an odd function and has horizontal asymptotes, approximate graphically the graph of its first derivative \( f'(x) \).

Solution to Question 2

The function \( f \) is increasing for all \( x \), so \[ f'(x) > 0 \quad \text{for all } x, \] and the graph of \( f'(x) \) lies above the \( x \)-axis.
The value \( f'(a) \) equals the slope of the tangent line to the graph of \( f \) at the point \( (a, f(a)) \). From the graph, the slope appears to be largest near the origin \( (0,0) \).

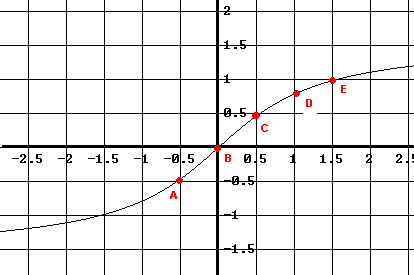
Approximation of derivative near the origin

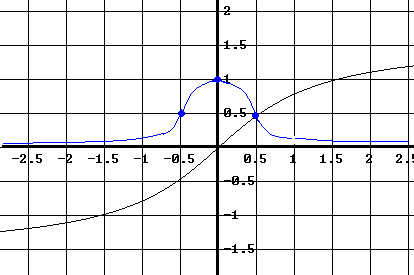
Using points \( A(x_A, y_A) \) and \( C(x_C, y_C) \) near the origin, \[ m_0 \approx \frac{y_C - y_A}{x_C - x_A} = \frac{0.5 - (-0.5)}{0.5 - (-0.5)} = 1 . \]
Using points \( C \) and \( E \), the slope near point \( D \) is approximated by \[ m_1 \approx \frac{1 - 0.5}{1.5 - 0.5} = 0.5 . \]
Since \( f \) has horizontal asymptotes, \[ \lim_{x \to \pm\infty} f'(x) = 0 . \]
Combining this information, a reasonable approximation of \( f'(x) \) is shown below in blue.

Question 3

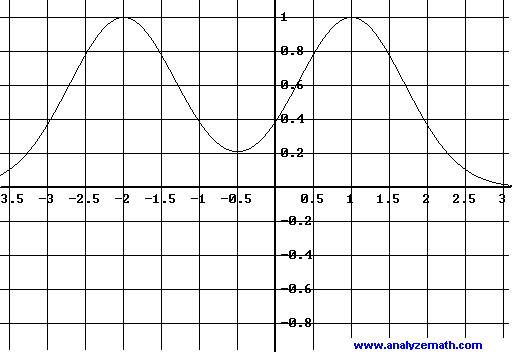
Approximate the graph of the first derivative \( f'(x) \) of the function \( f \) shown below. Assume that the graph of \( f \) is symmetric with respect to the vertical line \[ x = -0.5 \] and that \( y = 0 \) is a horizontal asymptote.

Solution to Question 3

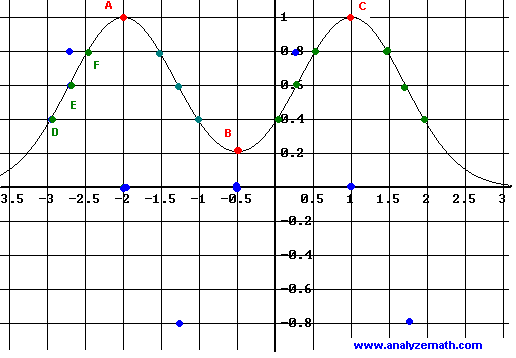
The derivative satisfies \[ f'(x) = 0 \quad \text{at} \quad x = -2,\; -0.5,\; 1, \] which correspond to the extrema of \( f \).
Using points \( D, E, F \), the slope at point \( E \) is approximated by \[ m_0 \approx \frac{0.8 - 0.4}{-2.4 - (-2.9)} = 0.8 . \]
Using the next group of three points to the right gives a slope close to \[ -0.8 . \] These values allow us to plot approximate points of \( f'(x) \).

Approximate derivative points for Question 3

The derivative is positive where \( f \) is increasing: \[ (-\infty, -2) \quad \text{and} \quad (-0.5, 1). \]
The derivative is negative where \( f \) is decreasing: \[ (-2, -0.5) \quad \text{and} \quad (1, +\infty). \]
A possible approximation of \( f'(x) \) is shown below in blue:

Final graph of derivative for Question 3