Derivatives of Even and Odd Functions

Question 1

The graph of an even function \(f\) is shown below:

Assuming \(f\) is differentiable everywhere, which of the graphs A), B), C), or D) represents \(f'(x)\)?

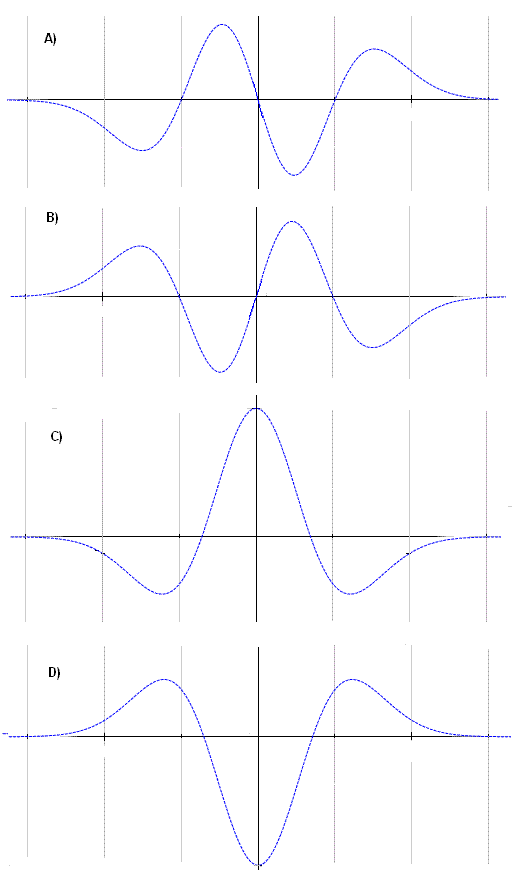
Solution:

The given function is even, so \[ f(x) = f(-x) \] Differentiating both sides: \[ \frac{d}{dx}f(x) = \frac{d}{dx}f(-x) \] Using the chain rule, let \(u = -x\): \[ \frac{d}{dx}f(-x) = \frac{df}{du} \cdot \frac{du}{dx} = f'(u) \cdot (-1) = -f'(-x) \] Substituting back: \[ f'(x) = -f'(-x) \quad \Rightarrow \quad f'(-x) = -f'(x) \] This proves the derivative of an even function is odd. Analyzing the graphs A)–D), only A) and B) are odd. Observing \(f\), it decreases from its maximum on the left to the origin, so the derivative in this interval must be negative. Therefore, the correct graph is B).

Question 2

The graph of an odd function \(f\) is shown below:

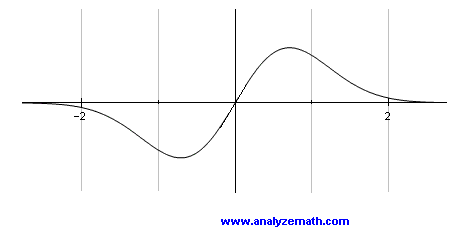
Assuming \(f\) is differentiable everywhere, which of the graphs A), B), C), or D) represents \(f'(x)\)?

Solution:

The given function is odd, so \[ f(x) = -f(-x) \] Differentiating both sides: \[ \frac{d}{dx}f(x) = - \frac{d}{dx} f(-x) \] Using the chain rule (\(u=-x\)): \[ \frac{d}{dx}f(-x) = f'(u) \cdot \frac{du}{dx} = f'(-x) \cdot (-1) = -f'(-x) \] Substituting back: \[ f'(x) = -(-f'(-x)) = f'(-x) \] Hence, the derivative of an odd function is even. Analyzing the graphs A)–D), only C) and D) are even. Observing \(f\) near the origin, it is increasing, so the derivative must be positive. Therefore, the correct graph is C).