Modulus and Argument of Complex Numbers
The modulus and argument of a Complex numbers are defined algebraically
and interpreted geometrically. Examples with detailed solutions are included.
A modulus and argument calculator may be used for more practice.
A complex number written in standard form as \( Z = a + ib \) may be plotted on a rectangular system of axis where the horizontal axis represent the real part of \( Z \) and the vertical axis represent
the imaginary part of \( Z \). The geometrical representation of complex numbers on a complex plane, also called Argand plane, is very similar to vector representation in rectangular systems of axes.

The modulus of a complex number in standard form \( Z = a + ib \) is defined by
\[ |z| = \sqrt{a^2 + b^2} \]
and its argument \( \theta \) is defined by
\[ \tan (\theta) = \left (\dfrac{b}{a} \right) \]
Note
Since the above trigonometric equation has an infinite number of solutions (since \( \tan \) function is periodic), there are two major conventions adopted for the range of \( \theta \) and let us call them conventions 1 and 2 for simplicity.
Convention (1) define the argument \( \theta \) in the range: \( 0 \le \theta \lt 2\pi \)
Convention (2) defines the argument \( \theta \) in the range : \( (-\pi, +\pi ] \)
The four quadrants , as defined in trigonometry, are determined by the signs of \( a \) and \( b\)
If the terminal side of \( Z \) is in quadrant (I) or (II) the two conventions give the same value of \( \theta \).
If the terminal side of \( Z \) is in quadrant (III) or (IV) convention one gives a positive angle and convention (2) gives a negative angle related by
In what follows, we use convention (1) where \( \theta \) is in the range: \( 0 \le \theta \lt 2\pi \) but we also mention convention (2).
The graphical interpretations of the modulus \( |Z| \) and the argument \( \theta \) are shown below for a complex number on a complex.
The modulus \( |Z| \) is the length of the segment representing the complex number. It may represent a magnitude if the complex number represent a physical quantity. The argument \( \theta \) is an angle in standard position (starting from the positive direction of the axis of the real part), representing the direction of \( Z \)
If we are given the modulus \( |Z| \) and argument \( \theta \) of a complex number \( Z \), then the standard form of \( Z \) is given by
\[ Z = |Z| \; ( \cos \theta + i \sin \theta ) \]
Example 1
Plot the complex number \( Z = -1 + i \) on the complex plane and calculate its modulus and argument.
Solution to Example 1
The complex number \(Z = -1 + i = a + i b \) hence
\( a = -1 \) and \( b = 1 \)
\( Z \) is plotted as a vector on a complex plane shown below with \( a = -1 \) being the real part and \( b = 1 \) being the imaginary part.
The modulus of \( Z \) , \( |Z| = \sqrt {a^2+b^2} = \sqrt {(-1)^2+(1)^2} = \sqrt 2\) is the length of the vector representing the complex number \( Z \).
The argument \( \theta \) is the angle in counterclockwise direction with initial side starting from the positive real part axis.
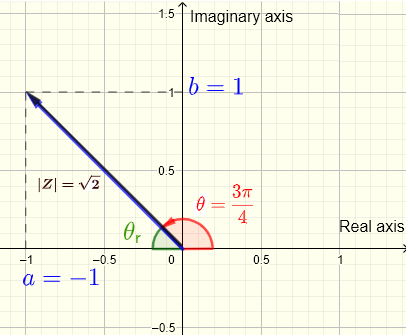
\( |Z| = \sqrt {a^2 + b^2} = \sqrt {(-1)^2 + 1^2} = \sqrt {1 + 1} = \sqrt 2\)
We first need to find the reference angle \( \theta_r \) which is the acute angle between the terminal side of \( \theta \) and the real part axis.
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1}\left|\dfrac{1}{-1}\right| =\tan^{-1} (1) = \dfrac{\pi}{4}\)
The real part of \(z\) is negative and its imaginary part is positive, hence the terminal side of \( \theta \) is in quadrant II (see plot of \( z \) above).
\( \theta \) is computed as follows:
\( \theta = \pi - \theta_r = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\)
Conclusion: Modulus: \( |Z| = \sqrt 2\) , argument: \( \theta = \dfrac{3\pi}{4}\)
Note Both conventions (1) and (2) (see definition above) give the same value for the argument \( \theta \).
Example 2
Calculate the modulus and argument of the complex numbers:
a) \( i \)
b) \( - 2 \)
c) \( - i \)
d) \( - 1 - 2i \)
e) \( 1 - i \)
Solution to Example 2
a)
Let \( Z = i = a + i b \)
gives \( a = 0 \) and \( b = 1 \)
Modulus: \( |Z| = \sqrt {0^2 + 1^2} = 1 \)
\( tan \theta = \dfrac{1}{0} = undefined \)
An angle with terminal side on the imaginary axis has a tangent that is undefined.
It is easier to determine the argument \( \theta = \dfrac{\pi}{2} \) from the plot of \( z = i \) shown below.
.png)
Note Both conventions (1) and (2) (see definition above) give the same value for the argument \( \theta \).
b)
Let \( Z = -2 = a + i b \)
gives \( a = -2 \) and \( b = 0 \)
Modulus: \( |Z| = \sqrt {(-2)^2 + 0^2} = 2 \)
\( tan \theta = \dfrac{0}{-2} = 0 \)
An angle with terminal side on the real axis has a tangent equal to 0.
We can determine that the argument of \( Z \): \( \theta = \pi \) from the plot of \( Z = -2 \) shown below.
.png)
Note Both conventions (1) and (2) (see definition above) give the same value for the argument \( \theta \).
c)
Let \( Z = - i = a + i b \)
gives \( a = 0 \) and \( b = - 1 \)
Modulus: \( |Z| = \sqrt {0^2 + (-1)^2} = 1 \)
\( tan \theta = \dfrac{-1}{0} = undefined \)
An angle whose tangent is undefined is an angle with terminal side on the imaginary axis.
We determine \( \theta = \dfrac{3\pi}{2} \) from the plot of \( z = - i \) shown below.
.png)
Note Conventions (2) gives \( \theta = \dfrac{3\pi}{2} - 2\pi = - \dfrac{\pi}{2}\).
d)
Let \( z = - 1 -2i = a + i b \)
gives \( a = -1 \) and \( b = - 2 \)
Modulus: \( |Z| = \sqrt {(-1)^2 + (-2)^2} = \sqrt 5 \)
Determine the reference angle: \( tan \theta_r = |\dfrac{-2}{-1}| = 2 \) , \( \theta_r = \arctan 2 \)
The argument of \( Z \) is: \( \theta = \pi + \theta_r = \pi + \arctan 2 \approx 4.25 \)
.png)
Note Convention (2) gives \( \theta = \pi + \arctan 2 - 2\pi = -\pi + \arctan 2 \approx -2.03444 \).
e)
Let \( Z = 1 - i = a + i b \)
gives \( a = 1 \) and \( b = - 1 \)
Modulus: \( |Z| = \sqrt {(1)^2 + (-1)^2} = \sqrt 2 \)
Determine the reference angle: \( tan \theta_r = |\dfrac{-1}{1}| = 1 \) , \( \theta_r = \dfrac{\pi}{4} \)
The argument of \( Z \) is: \( \theta = 2\pi - \theta_r = 2\pi - \dfrac{\pi}{4} = \dfrac{7\pi}{4} \)
.png)
Note Convention (2) gives \( \theta = \dfrac{7\pi}{4} - 2\pi = - \dfrac{\pi}{4} \).
Example 3
Plot each of the complex number given by its modulus and argument and write it in standard form.
a) \( |Z_1| = 3 \) , \( \theta_1 = 0 \)
b) \( |Z_2| = 4 \) , \( \theta_2 = 135^{\circ} \)
c) \( |Z_3| = 2 \) , \( \theta_3 = \dfrac{7\pi}{6} \)
b) \( |Z_4| = 2.5 \) , \( \theta_4 = 300^{\circ} \)
Solution to Example 3
The plot of all given complex numbers is shown below.

Write in standard form.
a) \( Z_1 = 3\cos 0 + 3 \sin 0 i = 3 \)
b) \( Z_2 = 4\cos 135^{\circ} + 3 \sin 135^{\circ} i \approx -2.88 + 2.88 i \)
c) \( Z_3 = 2\cos \dfrac{7\pi}{6} + 2 \sin \dfrac{7\pi}{6} i \approx - 1.73 - i \)
c) \( Z_3 = 2\cos \dfrac{7\pi}{6} + 2 \sin \dfrac{7\pi}{6} i \approx 1.25 - 2.17 i \)
You may also review De Moivre's Theorem Power and Root of Complex Numbers.
Questions
1) Calculate the modulus and argument (in degrees and radians) of the complex numbers.
- \( z_1 = - 1 \)
- \( z_2 = - 2 i \)
- \( z_3 = -\sqrt 3 - i \)
- \( z_4 = - 3 + 3\sqrt 3 i \)
- \( z_5 = 7 - 7 i \)
.
2) Write in standard form the complex numbers given by their modulus and argument. .
- \( |Z_1| = 0.5 \) , \( \theta_1 = 2.1 \)
- \( |Z_2| = 3.4 \) , \( \theta_2 = \pi/2 \)
- \( |Z_3| = 4 \) , \( \theta_3 = 0 \)
- \( |Z_4| = 12 \) , \( \theta_4 = 122^{\circ} \)
- \( |Z_5| = 200 \) , \( \theta_5 = 5\pi/3 \)
- \( |Z_6| = 3/7 \) , \( \theta_6 = 330^{\circ} \)
.
Solutions to the Above Questions
1)
- \( |z_1| = 1 \) , \( \theta_1 = \pi \) or \( \theta_1 = 180^{\circ} \) convention(2) gives the same values for the argument
- \( |z_2| = 2 \) , \( \theta_2 = 3\pi/2 \) or \( \theta_2 = 270^{\circ} \) convention(2) gives: \( - \pi/2 \) or \( -90^{\circ} \)
- \( |z_3| = 2 \) , \( \theta_3 = 11 \pi/6 \) or \( \theta_3 = 330^{\circ} \) convention(2) gives: \( - \pi/6 \) or \( -30^{\circ} \)
- \(| z_4 | = 6 \) , \( \theta_4 = 2\pi/3\) or \( \theta_4 = 120^{\circ}\) convention(2) gives same values for the argument.
- \(| z_5 | = 2 \sqrt 7 \) , \( \theta_5 = 7\pi/4\) or \( \theta_5 = 315^{\circ}\) convention(2) gives: \( - \pi/4 \) or \( -45^{\circ} \)
.
2)
- \( Z_1 = 0.5 (\cos 2.1 + i \sin 2.1) \approx 0.18 + 0.43 i\)
- \( Z_2 = 3.4 (\cos \pi/2 + i \sin \pi/2) = - 3.4 i\)
- \( Z_3 = 4 (\cos 0 + i \sin 0) = 4\)
- \( Z_4 = 12 (\cos 122^{\circ} + i \sin 122^{\circ} ) \approx -6.36 + 10.18 i\)
- \( Z_5 = 200 (\cos 5\pi/3 + i \sin 5\pi/3 )= 100-100\sqrt{3} i\)
- \( Z_6 = (3/7) (\cos 330^{\circ} + i \sin 330^{\circ} ) = \dfrac{3\sqrt{3}}{14}- \dfrac{3}{14} i \)
.
More References and Links
Modulus and Argument of a Complex Number - Calculator
Convert a Complex Number to Polar and Exponential Forms Calculator
Complex Numbers in Polar Form
Euler's formula.
Complex Numbers - Basic Operations
Find the Reference Angle
Sum and Difference Formulas in Trigonometry
Convert a Complex Number to Polar and Exponential Forms - Calculator
Algebra and Trigonometry - R. E. LARSON, R. P. Hostetler, B. H. Edwards, D.E Heyd,
Houghton Mifflin Company - ISBN: 0-669-41723-8



.png)
.png)
.png)
.png)
.png)
