In the study of compound interest, it is shown that if an amount of money \( P \) (the principal) is invested at an annual interest rate \( r \), then the total amount \( A \) after \( t \) years is
\[ A = P(1 + r)^t \]If the interest is compounded \( n \) times per year, the amount becomes
\[ A = P\left(1 + \frac{r}{n}\right)^{nt} \]Let \[ N = \frac{n}{r} \] so that \( \frac{r}{n} = \frac{1}{N} \) and \( n = rN \). Substituting into the formula gives
\[ A = P\left(1 + \frac{1}{N}\right)^{Nrt} \]This expression can be rewritten as
\[ A = P\left( \left(1 + \frac{1}{N}\right)^N \right)^{rt} \]A natural question arises: what happens if the number of compoundings \( n \) (and therefore \( N \)) increases without bound?
As \( N \to \infty \), the quantity \[ \left(1 + \frac{1}{N}\right)^N \] approaches a constant value called Euler’s number, denoted by \( e \), named after the Swiss mathematician Leonhard Euler.
Numerically, \[ e \approx 2.71828182846 \]
The table below shows how the expression \( \left(1 + \frac{1}{N}\right)^N \) approaches \( e \) as \( N \) increases.
| \( N \) | \( \left(1 + \frac{1}{N}\right)^N \) |
|---|---|
| 1 | 2.00000 |
| 2 | 2.25000 |
| 3 | 2.37037 |
| 10 | 2.59374 |
| 20 | 2.65329 |
| 40 | 2.68506 |
| 100 | 2.70481 |
| 200 | 2.71149 |
| 400 | 2.71488 |
The graph below illustrates \( y = \left(1 + \frac{1}{N}\right)^N \) as a function of \( N \). As \( N \) increases, the curve approaches the horizontal line \( y = e \).
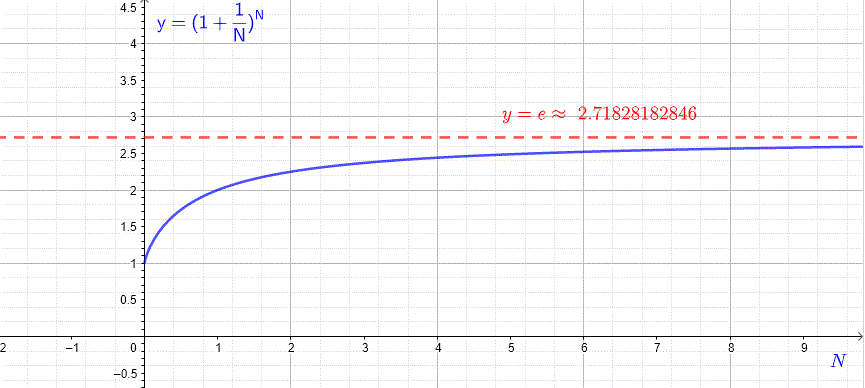
More rigorously, Euler’s number is defined by the limit
\[ e = \lim_{N \to \infty} \left(1 + \frac{1}{N}\right)^N \]Letting \( m = \frac{1}{N} \), an equivalent definition is
\[ e = \lim_{m \to 0} (1 + m)^{\frac{1}{m}} \]When interest is compounded continuously, the amount of money after \( t \) years is given by
\[ A = Pe^{rt} \]Euler’s number \( e \) plays a central role in applied mathematics. Many models in physics, engineering, chemistry, economics, and population dynamics are expressed using exponential functions with base \( e \).
The natural exponential function is defined by
\[ f(x) = e^x \]Its inverse function, the natural logarithm, is defined by
\[ g(x) = \ln(x) \]The graphs of the natural exponential and natural logarithmic functions are shown below.
