Fractions and Mixed Numbers
Examples on fractions and mixed numbers along with more questions and their solutions are presented.
The fractions and like fractions are defined using examples.
The naming and saying of a list of fractions is presented as an example.
The definition of proper and improper fractions , mixed numbers , the relationship between improper fractions and mixed numbers are also included.
Equivalent fractions,
the evaluation of fractions of quantities
and the
reduction of fractions are also included.
What Are Fractions?
A fraction is used to express part of a whole. It may be written in the form
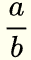 where
where 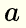 is called the numerator and
is called the numerator and 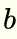 is called the denominator.
is called the denominator.
Example 1
You have a wire and you cut it into 4 equal parts as shown in the diagram below. Each small part has a length of 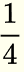 of the whole length represented by "1" divided by "4".
of the whole length represented by "1" divided by "4".

You now take 3 parts (in red) of the 4 parts as shown in the diagram below

This (red part) is represented mathematically as a fraction and written
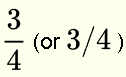 . The denominator of this fraction is 4 and the numerator is 3.
. The denominator of this fraction is 4 and the numerator is 3.
Example 2
You have large square piece of paper that you cut into 8 equal parts as shown below. Each small part has an area
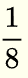 of the area of the whole square.
of the area of the whole square.
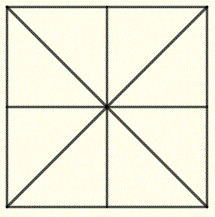
You now paint (in red) 5 of the 8 parts red as shown in the diagram below.

The painted part of the whole paper is represented diagrammatically by 5 small parts and mathematically as a fraction written as
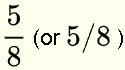 . The denominator of this fraction is 8 and the numerator is 5.
. The denominator of this fraction is 8 and the numerator is 5.
Notes:
1) Fractions with the same denominator are called like fractions .
2) A fraction cannot have denominator equal to zero as it is undefined.
\( \) \( \) \( \)
Naming and "Saying" Fractions
\( \displaystyle \frac{1}{2} \) : one half , 1 over 2
\( \displaystyle \frac{1}{3} \) : one third , 1 over 3
\( \displaystyle \frac{1}{4} \) : one-fourth (or a quarter) , 1 over 4
\( \displaystyle \frac{1}{5} \) : one-fifth , 1 over 5
\( \displaystyle \frac{1}{6} \) : one-sixth , 1 over 6
\( \displaystyle \frac{1}{7} \) : one-seventh , 1 over 7
\( \displaystyle \frac{1}{8} \) : one-eighth , 1 over 8
\( \displaystyle \frac{1}{9} \) : one-ninth , 1 over 9
\( \displaystyle \frac{1}{10} \) : one-tenth , 1 over 10
\( \displaystyle \frac{2}{3} \) : two-thirds , 2 over 3
\( \displaystyle \frac{3}{5} \) : three-fifths, 3 over 5
\( \displaystyle \frac{5}{6} \) : five-sixths , 5 over 6
\( \displaystyle \frac{3}{2} \) : three-halves , 3 over 2
\( \displaystyle \frac{8}{11} \) : eight-elevenths , 8 over 11
\( \displaystyle \frac{3}{8} \) : three-eighths , 3 over 8
Proper and Improper Fractions
A fraction with the numerator less than the denominator is called a proper fraction; otherwise it is called an improper fraction.
Example 3
The following are proper fractions: \( \displaystyle \frac{1}{2} \) , \( \displaystyle \frac{3}{4} \) , \( \displaystyle \frac{12}{23} \)
The following are improper fractions: \( \displaystyle \frac{2}{2} \) , \( \displaystyle \frac{6}{5} \) , \( \displaystyle \frac{25}{24} \)
Mixed Numbers
The sum of a whole number and a proper fraction is called a mixed number.
Example 4
Let us assume that each square in the diagram below represents one unit. There are 3 whole squares (or units) painted red plus a fraction of \( \displaystyle \frac{3}{4} \) also painted red. Using mixed numbers, the total area painted red is:
\( 3 \) units + \( \displaystyle \frac{3}{4} \) of one unit or simply written as a mixed number as follows: \[ \quad 3 \displaystyle \frac{3}{4} \]

Relationship Between Improper Fractions and Mixed Numbers
Another way of representing the area painted red in the diagram above is to split each of the 3 units into 4 equal parts as shown in the diagram below. We now count the total number of the (small) equal parts and express the area in read using improper fractions as
\[ \displaystyle \frac{15}{4} \]

In the above example the relationship between the mixed number and improper fraction is
\( \displaystyle \frac{15}{4} = 3 \displaystyle \frac{3}{4} \)
1 - How Convert a mixed number into an improper fraction?
Example 5
Convert \( 3 \displaystyle \frac{3}{4} \) into an improper fraction.
Solution to Example 5
Write the mixed number as a sum of a whole number and a fraction
\( 3 \displaystyle \frac{3}{4} = 3 + \displaystyle \frac{3}{4}\)
then convert the whole number into a fraction using the same denominator 4 as the fraction
\( 3 = \displaystyle \frac{12}{4} \)
We now add the two fractions
\( 3 \displaystyle \frac{3}{4} = 3 + \displaystyle \frac{3}{4} = \displaystyle \frac{12}{4} + \displaystyle \frac{3}{4} = \displaystyle \frac{15}{4}\)
2 - How Convert an improper fraction into a Mixed Number?
Example 6
Convert the improper fraction \( \displaystyle \frac{15}{4} \) into a mixed number.
Solution to Example 6
To convert \( \displaystyle \frac{15}{4} \) into a mixed number, first divide \(15\) by \(4\) using the long division.
The quotient of the division is the whole number, the remainder of the division is the numerator of the fraction and the denominator of the fraction is the divisor 4.
Divide 15 by 4, you get a quotient 3 and a remainder equal to 3. Hence
\( \displaystyle \frac{15}{4} = quotient + \displaystyle \frac{remainder}{4} = 3 + \displaystyle \frac{3}{4} = 3\displaystyle \frac{3}{4}\)
Comparing Fractions
Comparing like fractions (fractions with the same denominator) is straightforward; we just compare the numerators.
Example 7
\( \displaystyle \frac{3}{8} > \displaystyle \frac{2}{8} \)
To compare fractions with different denominators, we first rewrite them with the same denominator and then compare them.
Example 7
Compare the fractions \( \displaystyle \frac{6}{5} \) and \( \displaystyle \frac{3}{2} \)
Step 1: Find the
lowest common multiple (LCM) of the denominators \( 5 \) and \( 2 \)
LCM of \( (5 \text { and } 2) = 10 \)
Rewrite each fraction with the common denominator equal to LCM
\( \displaystyle \frac{6}{5} = \displaystyle \frac{6\times 2}{5\times2} = \displaystyle \frac{12}{10} \)
\( \displaystyle \frac{3}{2} = \displaystyle \frac{3\times5}{2\times5} = \displaystyle \frac{15}{10} \)
Hence comparing numerators we deduce that
\( \displaystyle \frac{6}{5} \lt \displaystyle \frac{3}{2} \)
Questions
- Represent each of the colored (in red) parts as fraction, a mixed number or both.
A whole circle is one unit.

A whole square is one unit.

A whole square is one unit.

A whole square is one unit.

- Which of the following is a proper fraction, improper or a mixed number?
a) \( \displaystyle \frac{1}{6} \) , b) \( 4\displaystyle \frac{3}{5} \) , c) \( \displaystyle \frac{7}{7} \) , d) \( \displaystyle \frac{12}{11} \) , e) \( \displaystyle \frac{0}{3} \) , f) \( 1\displaystyle \frac{9}{13} \)
- Convert the given improper fractions into mixed numbers.
a) \( \displaystyle \frac{10}{6} \) , b) \( \displaystyle \frac{123}{11} \) , c) \( \displaystyle \frac{4}{3} \)
- Convert the given mixed numbers into improper fractions.
a) \( 2\displaystyle \frac{1}{6} \) , b) \( 2\displaystyle \frac{2}{5} \) , c) \( 1\displaystyle \frac{4}{9} \)
- Order the following fractions and mixed numbers from smallest to largest.
a) \( 5\displaystyle \frac{1}{6} \) , b) \( \displaystyle \frac{21}{5} \) , c) \( 3\displaystyle \frac{4}{9} \)
Solutions to the Exercises
-
- As an improper fraction: \( \displaystyle \frac{9}{4} \) or a mixed number: \( 2 \displaystyle \frac{1}{4} \)
- As a proper fraction: \( \displaystyle \frac{7}{8} \)
- As an improper fraction: \( \displaystyle \frac{8}{8} \) or a whole number: \( 1 \)
- As an improper fraction: \( \displaystyle \frac{21}{8} \) or a mixed number: \( 2 \displaystyle \frac{5}{8} \)
-
Proper fractions: a) and e)
Improper fractions: c) and d)
Mixed numbers: b) and f)
-
a) \( \displaystyle \frac{10}{6} = 1 \frac{4}{6} = 1 \frac{2}{3}\)
b) \( \displaystyle \frac{123}{11} = 11 \frac{2}{11} \)
c) \( \displaystyle \frac{4}{3} = 1 \frac{1}{3} \)
-
a) \( 2\displaystyle \frac{1}{6} = \frac{13}{6} \)
b) \( 2\displaystyle \frac{2}{5} = \frac{12}{5} \)
c) \( 1\displaystyle \frac{4}{9} = \frac{13}{9} \)
-
Convert mixed number into improper fractions then convert all fractions to the same denominator using the LCM of the denominators: 6, 5 and 9.
a) \( 5\displaystyle \frac{1}{6} = \frac{31}{6} = \frac{31 \times 15}{6 \times 15} = \frac{465}{90} \)
b) \( \displaystyle \frac{21}{5} = \frac{21 \times 18}{5 \times 18 } = \frac{378}{90} \)
c) \( 3\displaystyle \frac{4}{9} = \frac{31}{9} = \frac{31 \times 10}{9 \times 10} = \frac{310}{90} \)
Order from smallest to largest: \( 3\displaystyle \frac{4}{9} , \quad \frac{21}{5} , \quad 5 \frac{1}{6} \)
More References and Links
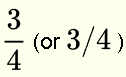 . The denominator of this fraction is 4 and the numerator is 3.
. The denominator of this fraction is 4 and the numerator is 3.


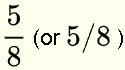 . The denominator of this fraction is 8 and the numerator is 5.
. The denominator of this fraction is 8 and the numerator is 5.





