What are Periodic Functions?
Periodic functions are applied to study signals and waves in electrical and electronic systems, vibrations in mechanical and civil engineering systems, waves in physics and wireless systems, and many other applications.
The graph of a periodic function repeats itself over cycles for \( x \) in the domain of the function. If \( f \) is known over one cycle, it is known everywhere over the domain of \( f \) since the graph repeats itself.
A function \( f \) is periodic with period \( P \) if:
\[ f(x) = f(x + P) \]for \( x \) in the domain of \( f \).
\( P \) is the smallest positive real number for which the above condition holds. In the graph below is shown a periodic function with two cycles as an example. The period \( P \) is the distance, along the x-axis, between any two points making a cycle:
\[ P = x_2 - x_1 = x_4 - x_3 \]
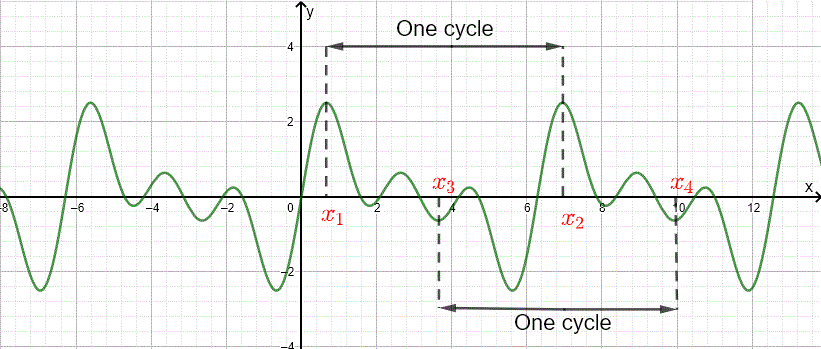
Example 1: Trigonometric Functions
All six trigonometric functions are periodic:
- \( \sin(x + 2\pi) = \sin(x) \), the period of \( \sin(x) \) is equal to \( P = 2\pi \).
The graph of \( \sin(x) \) is shown below with one cycle, in red, whose length over the x-axis is equal to one period \( P \): \( P = 2\pi - 0 = 2\pi \)
.gif)
- \( \cos(x + 2\pi) = \cos(x) \), the period of \( \cos(x) \) is equal to \( P = 2\pi \).
- \( \sec(x + 2\pi) = \sec(x) \), the period of \( \sec(x) \) is equal to \( P = 2\pi \).
- \( \csc(x + 2\pi) = \csc(x) \), the period of \( \csc(x) \) is equal to \( P = 2\pi \).
- \( \tan(x + \pi) = \tan(x) \), the period of \( \tan(x) \) is equal to \( P = \pi \).
The graph of \( \tan(x) \) is shown below with one cycle, in red, whose length over the x-axis is equal to one period \( P \): \( P = \dfrac{\pi}{2} - \left(-\dfrac{\pi}{2}\right) = \pi \)
.gif)
- \( \cot(x + \pi) = \cot(x) \), the period of \( \cot(x) \) is equal to \( P = \pi \).
Period of Transformed Functions
- If \( P \) is the period of \( f(x) \), then the period of \( A f(b x + c) + D \) is given by \( \dfrac{P}{|b|} \).
- If \( P \) is the period of \( f(x) \), then \( f(x + n P) = f(x) \) for any integer \( n \).
Examples with Detailed Solutions
Example 2
Use the period of the trigonometric functions given in Example 1 to find the period of each function given below:
- \( f(x) = \sin(0.5 x) \)
- \( g(x) = \tan(2 x + \pi/6) \)
- \( h(x) = \cos(-(2/3) x - \pi) \)
- \( j(x) = \sec(\pi x - 2) \)
- \( k(x) = \cot(-(2\pi/3) x) \)
View Solutions
- The period of \( \sin(x) \) is \( 2\pi \). Using the formula, the period of \( f(x) = \sin(0.5 x) \) is: \[ \dfrac{2\pi}{|0.5|} = 4\pi \]
- The period of \( \tan(x) \) is \( \pi \), hence the period of \( g(x) = \tan(2 x + \pi/6) \) is equal to: \[ \dfrac{\pi}{|2|} = \frac{\pi}{2} \]
- The period of \( \cos(x) \) is \( 2\pi \), hence the period of \( h(x) = \cos(-(2/3) x - \pi) \) is equal to: \[ \dfrac{2\pi}{|-2/3|} = 3\pi \]
- The period of \( \sec(x) \) is \( 2\pi \) and the period of \( j(x) = \sec(\pi x - 2) \) is given by: \[ \dfrac{2\pi}{|\pi|} = 2 \]
- The period of \( \cot(x) \) is \( \pi \) and the period of \( k(x) = \cot(-(2\pi/3) x) \) is given by: \[ \dfrac{\pi}{|-2\pi/3|} = \frac{3}{2} \]
Example 3
Find the period of each of the functions given below:
- \( f(x) = \sin(x) \cos(x) \)
- \( g(x) = \sin^2(x) \)
- \( h(x) = \cos(x) + \sin(x) \)
View Solutions
- Use the identity \( \sin(2x) = 2 \sin(x) \cos(x) \) to write \( f(x) = \sin(x) \cos(x) = \dfrac{1}{2} \sin(2x) \). Hence, the period of \( f(x) \) is given by: \[ \dfrac{2\pi}{|2|} = \pi \]
- Use the identity \( \cos(2x) = 1 - 2 \sin^2(x) \) (or \( \sin^2(x) = \dfrac{1 - \cos(2x)}{2} \)) to write \( g(x) = \sin^2(x) = \dfrac{1}{2} - \dfrac{1}{2} \cos(2x) \). Hence, the period of \( g(x) \) is given by: \[ \dfrac{2\pi}{|2|} = \pi \]
- Rewrite \( h(x) = \cos(x) + \sin(x) \) by factoring out \( \sqrt{1^2 + 1^2} = \sqrt{2} \): \[ h(x) = \sqrt{2} \left( \frac{1}{\sqrt{2}}\cos(x) + \frac{1}{\sqrt{2}}\sin(x) \right) = \sqrt{2} \sin(x + \pi/4) \] Calculate the period of \( h(x) \) as: \[ \dfrac{2\pi}{|1|} = 2\pi \]