Definitionsbereich einer Quadratwurzelfunktion
Wie findet man den Definitionsbereich
von Quadratwurzelfunktionen? Es werden mehrere Beispiele zusammen mit detaillierten Lösungen und Erklärungen mit grafischen Darstellungen und Interpretation des Definitionsbereichs vorgestellt.
Den Definitionsbereich einer Quadratwurzelfunktion finden
Wir müssen zuerst verstehen, dass \( \sqrt x \) nur reell ist, wenn das Argument \( x \), also die Größe unter der Wurzel \( \sqrt{} \), die Bedingung erfüllt: \( x \ge 0 \). Dies kann leicht überprüft werden, indem man den Graphen von \( y = \sqrt x \) betrachtet, der unten gezeigt wird: Der Graph existiert nur für \( x \ge 0 \).

Beispiele mit ihren Lösungen
Beispiel 1
Finden Sie den Definitionsbereich der Funktion \[ f(x) = \sqrt{x - 2} \]
Lösung
\( f(x) = \sqrt{x - 2} \) nimmt reelle Werte an, wenn das Argument \( x - 2 \), also die Größe unter der Wurzel \( \sqrt{} \), die Bedingung erfüllt: \( x - 2 \ge 0 \). Die Lösung der Ungleichung ist
\[ x \ge 2 \]
welches der Definitionsbereich der Funktion ist, und dies kann grafisch überprüft werden, wie unten gezeigt, wo der Graph von \( f\) für \( x \ge 2 \) "existiert".

Beispiel 2
Finden Sie den Definitionsbereich der Funktion \[ f(x) = \sqrt{|x - 1|} \]
Lösung
\( f(x) = \sqrt{|x - 1|} \) nimmt reelle Werte an, wenn das Argument \( |x - 1| \), also die Größe unter der Wurzel \( \sqrt{} \), die Bedingung erfüllt: \( |x - 1| \ge 0 \). Die Lösung der Ungleichung ist
alle reellen Zahlen, weil der Absolutwertausdruck \( |x - 1| \) für \( x = 1 \) immer positiv oder null ist.
Der Definitionsbereich der Funktion ist die Menge der reellen Zahlen \( \mathbb{R} \), und dies kann grafisch überprüft werden, wie unten gezeigt, wo der Graph von \( f\) für alle \( x \)-Werte "existiert".

Beispiel 3
Finden Sie den Definitionsbereich der Funktion \[ f(x) = \dfrac{1}{ \sqrt{x + 3}} \].
Lösung
Unter Berücksichtigung, dass die Funktion das Verhältnis zweier Funktionen ist und dass eine Division durch Null nicht erlaubt ist, nimmt die gegebene Funktion reelle Werte an, wenn das Argument \( x + 3 \), also die Größe unter der Wurzel \( \sqrt{} \), die Bedingung erfüllt: \( x + 3 \gt 0 \). Beachten Sie, dass das verwendete Ungleichheitszeichen \( \gt \) und nicht \( \ge \) ist, weil wir keine Null im Nenner haben wollen. Die Lösung der Ungleichung ist
\[ x \gt - 3 \]
Der Definitionsbereich der Funktion ist die Menge der reellen Zahlen größer als -3, und dies kann grafisch überprüft werden, wie unten gezeigt, wo der Graph von \( f\) für alle \( x > - 3\) Werte "existiert".

Beispiel 4
Finden Sie den Definitionsbereich der Funktion \[ f(x) = \dfrac{\sqrt{x + 4}}{ \sqrt{x - 2}} \]
Lösung
Die gegebene Funktion nimmt reelle Werte an, wenn zwei Bedingungen erfüllt sind.
1) \( x + 4 \ge 0 \) , Null ist im Zähler erlaubt, daher die Verwendung des Ungleichheitszeichens \( \ge \).
und
2) \( x - 2 \gt 0 \) , Null ist im Nenner NICHT erlaubt, daher die Verwendung des Ungleichheitszeichens \( \gt \).
Der Definitionsbereich der Funktion ist die Schnittmenge der beiden Lösungsmengen der obigen Ungleichungen.
\[ x \ge - 4 \quad \text{und} \quad x \gt 2 \]
Die Schnittmenge der beiden obigen Lösungsmengen ist.
\[ x \gt 2 \]
Welches der Definitionsbereich der gegebenen Funktion ist, wie unten im Graphen von \( f \) gezeigt.

Beispiel 5
Finden Sie den Definitionsbereich der Funktion \( f(x) = \sqrt{\dfrac{x + 4}{ {x - 2}}} \).
Lösung
Die gegebene Funktion nimmt reelle Werte an, wenn
\[ \dfrac{x + 4}{ {x - 2}} \ge 0 \]
Wir müssen die obige Ungleichung lösen. Die Nullstellen des Zählers und Nenners sind
\[ x = - 4 \quad \text{und} \quad x = 2 \]
Die Nullstellen teilen den Zahlenstrahl in 3 Intervalle, über die das Vorzeichen der Ungleichung gleich bleibt. Daher die Intervalle.
\[ (-\infty , -4) \; , \; (-4 , 2 ) \; , \; (2 , \infty) \]
Wir wählen einen Wert innerhalb jedes Intervalls und verwenden ihn, um das Vorzeichen des Ausdrucks \[ \dfrac{x + 4}{ {x - 2}} \] zu bestimmen.
1) Im Intervall \( (-\infty , -4) \) wählen Sie \( x = -6 \) und setzen \( x \) in \( \dfrac{x + 4}{ {x - 2}} \) ein, um dessen Vorzeichen zu bestimmen
\[ \dfrac{ -6 + 4}{ {-6 - 2}} \gt 0 \]
2) Im Intervall \( (-4 , 2) \) wählen Sie \( x = 0 \) und setzen \( x \) in \( \dfrac{x + 4}{ {x - 2}} \) ein, um dessen Vorzeichen zu bestimmen
\[ \dfrac{ 0 + 4}{ {0 - 2}} \lt 0 \]
3) Im Intervall \( (2 , \infty) \) wählen Sie x = 3 und setzen \( x \) in \( \dfrac{x + 4}{ {x - 2}} \) ein, um dessen Vorzeichen zu bestimmen
\[ \dfrac{ 3 + 4}{ {3 - 2}} \gt 0 \]
Daher ist der Definitionsbereich die Vereinigung aller Intervalle, in denen \( \dfrac{x + 4}{ {x - 2}} \gt 0 \) gilt, und ist gegeben durch.
\[ (-\infty , -4] \cup (2 , \infty) \]
Der Graph von \( f \) ist wie unten gezeigt, und wir können den oben gefundenen Definitionsbereich leicht überprüfen. Beachten Sie, dass \( x = 2 \) nicht im Definitionsbereich liegt, weil die Division durch Null nicht erlaubt ist.

Beispiel 6
Finden Sie den Definitionsbereich der Funktion \[ f(x) = \sqrt{-x^2-4} \]
Lösung
Die gegebene Funktion nimmt reelle Werte an, wenn
\[ -x^2 - 4 \ge 0 \]
Der Ausdruck \( x^2 + 4 \) ist die Summe eines Quadrats und einer positiven Zahl. Somit
\[ x^2 + 4 \ge 0 \]
Multiplizieren Sie alle Terme der obigen Ungleichung mit -1 und ändern Sie das Ungleichheitszeichen, um zu erhalten
\[ - x^2 - 4 \le 0 \]
Daher ist der Definitionsbereich der gegebenen Funktion eine leere Menge, und die gegebene Funktion hat keinen Graphen. Versuchen Sie, ihn mit einem Grafikrechner zu zeichnen.
Beispiel 7
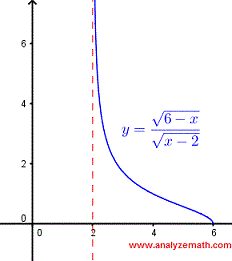
Finden Sie den Definitionsbereich der Funktion \[ f(x) = \dfrac{\sqrt{6 - x}}{ \sqrt{x - 2}} \]
Lösung
Die gegebene Funktion nimmt reelle Werte an, wenn zwei Bedingungen erfüllt sind.
1) \( 6 - x \ge 0 \) , Null ist im Zähler erlaubt, daher die Verwendung des Ungleichheitszeichens \( \ge \).
und
2) \( x - 2 \gt 0 \) , Null ist im Nenner nicht erlaubt, daher die Verwendung des Ungleichheitszeichens \( \gt \).
Der Definitionsbereich der Funktion ist die Schnittmenge der beiden Lösungsmengen der obigen Ungleichungen
\[ x \le 6 \quad \text{und} \quad x \gt 2 \]
Die Schnittmenge der beiden obigen Lösungsmengen ist durch das Intervall gegeben.
\[ (2 , 6] \]
Der Graph von \( f \) ist wie unten gezeigt, und wir können den oben gefundenen Definitionsbereich leicht überprüfen. Beachten Sie, dass x = 2 nicht im Definitionsbereich liegt, weil die Division durch Null nicht erlaubt ist.
Beispiel 8
Finden Sie den Definitionsbereich der Funktion \[ f(x) = \sqrt{x^2 - 4} \]
Lösung
Die gegebene Funktion nimmt reelle Werte an, wenn
\[ x^2 - 4 \ge 0\] was auch geschrieben werden kann als \[ (x - 2)(x + 2) \ge 0 \]
Die Lösungsmenge für die obige quadratische Ungleichung ist durch das Intervall gegeben
\[ (-\infty , -2] \cup [2 , \infty) \]
Der Graph von \( f \) ist wie unten gezeigt, und wir können den oben gefundenen Definitionsbereich leicht überprüfen.

Beispiel 9
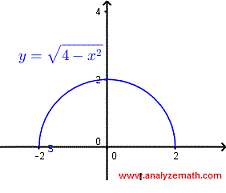
Finden Sie den Definitionsbereich der Funktion \( f(x) = \sqrt{4 - x^2} \).
Lösung
Die gegebene Funktion nimmt reelle Werte an, wenn
\[ 4 - x^2 \ge 0\] was auch geschrieben werden kann als \[ (2 - x)(2 + x) \ge 0\]
Die Lösungsmenge für die obige quadratische Ungleichung ist durch das Intervall gegeben
\[ [-2 , 2] \]
Der Graph von \( f \) ist wie unten gezeigt, und wir können den oben gefundenen Definitionsbereich leicht überprüfen.
Weitere Referenzen und Links
Startseite









