Wie findet man den Definitionsbereich von rationalen Funktionen? Es werden Beispiele mit detaillierten Lösungen und Erklärungen sowie einer grafischen Interpretation vorgestellt.
Wir müssen zuerst verstehen, dass \( \dfrac{1}{x} \) nur dann reelle Werte annimmt, wenn der Nenner ungleich Null ist. Das heißt, \( x \ne 0 \).
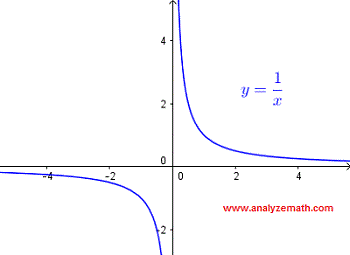
Diese Einschränkung lässt sich leicht überprüfen, indem man den Graphen der Funktion \( y = \dfrac{1}{x} \), der unten abgebildet ist, betrachtet. Der Graph "existiert" für alle Werte von \( x \) außer bei \( x = 0 \), wo die Funktion nicht definiert ist.
Der Definitionsbereich von \( \dfrac{1}{x} \), in Intervallschreibweise, ist gegeben durch:
\[ (-\infty , 0) \cup (0 , \infty) \]

Die gegebene Funktion nimmt reelle Werte an und ist daher für alle Werte von \( x \) definiert und reell, außer wenn der Nenner Null ist.
Das ist der Fall, wenn:
\[ x - 2 \ne 0 \quad \Rightarrow \quad x \ne 2 \]In Intervallschreibweise ist der Definitionsbereich der Funktion:
\[ (-\infty , 2) \cup (2 , \infty) \]Der Graph der Funktion \( f(x) = \dfrac{1}{x - 2} \) ist unten dargestellt. Die Funktion ist bei \( x = 2 \) nicht definiert, was im Graphen deutlich als vertikale Asymptote zu erkennen ist.

Die gegebene Funktion nimmt reelle Werte an und ist daher reell, wenn:
\[ (x - 1)(x + 2) \ne 0 \]Diese Ungleichung gilt, wenn \( x \ne 1 \) und \( x \ne -2 \).
In Intervallschreibweise ist der Definitionsbereich der Funktion:
\[ (-\infty , -2) \cup (-2 , 1) \cup (1 , \infty) \]Unten ist der Graph der Funktion \( f(x) = \dfrac{x + 3}{(x - 1)(x + 2)} \) abgebildet, und wir können beobachten, dass die Funktion bei \( x = -2 \) und \( x = 1 \) nicht definiert ist. An diesen Stellen haben wir vertikale Asymptoten.

Die gegebene Funktion nimmt reelle Werte an und ist daher definiert und reell, wenn der Nenner nicht gleich Null ist:
\[ x^2 - 4 \ne 0 \]Faktorisieren Sie \( x^2 - 4 \) und schreiben Sie die Ungleichung um als:
\[ (x - 2)(x + 2) \ne 0 \]Der Ausdruck \( (x - 2)(x + 2) \) ist ungleich Null, wenn:
\[ x \ne -2 \quad \text{und} \quad x \ne 2 \]In Intervallschreibweise ist der Definitionsbereich der Funktion gegeben durch:
\[ (-\infty , -2) \cup (-2 , 2) \cup (2 , \infty) \]Unten ist der Graph der Funktion \( f(x) = \frac{1}{x^2 - 4} \) abgebildet, und wir können sehen, dass die Funktion bei \( x = -2 \) und \( x = 2 \) nicht definiert ist:
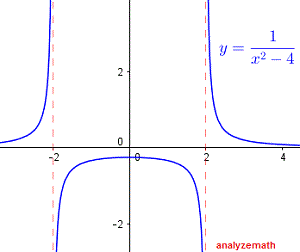
Die gegebene Funktion nimmt reelle Werte an und ist daher reell, wenn:
\[ x^2 + x - 2 \ne 0 \]Faktorisieren Sie \( x^2 + x - 2 \) und schreiben Sie die Ungleichung um als:
\[ (x - 1)(x + 2) \ne 0 \]Der Ausdruck \( (x - 1)(x + 2) \) ist ungleich Null, wenn \( x \ne 1 \) und \( x \ne -2 \).
In Intervallform ist der Definitionsbereich gegeben durch:
\[ (-\infty, -2) \cup (-2, 1) \cup (1, \infty) \]Unten ist der Graph der Funktion \( f \) dargestellt, und wir können sehen, dass die gegebene Funktion bei \( x = -2 \) und \( x = 1 \) nicht definiert ist.
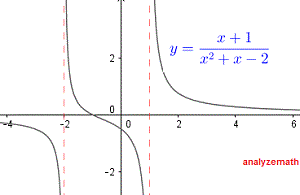
Die gegebene Funktion nimmt reelle Werte an und ist daher reell, wenn:
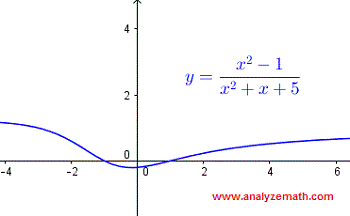
\[ x^2 + x + 5 \ne 0 \]Der Ausdruck \( x^2 + x + 5 \) kann über den reellen Zahlen nicht faktorisiert werden. Wir lösen daher die quadratische Gleichung mit der Diskriminante \( \Delta \):
\[ x^2 + x + 5 = 0 \] \[ \Delta = b^2 - 4ac = (1)^2 - 4(1)(5) = -19 \]Die Diskriminante ist negativ, also gibt es keine reellen Werte von \( x \), die den Ausdruck \( x^2 + x + 5 \) gleich Null machen. Somit ist der Definitionsbereich der Funktion die Menge aller reellen Zahlen.
In Intervallschreibweise ist der Definitionsbereich:
\[ (-\infty, \infty) \]Unten ist der Graph der Funktion \( f(x) = \dfrac{x^2 - 1}{x^2 + x + 5} \) abgebildet, und wir können sehen, dass sie für alle reellen Werte von \( x \) definiert ist.