1) Zeichnen Sie den Graphen der Umkehrfunktion von \( f \) in dasselbe Koordinatensystem.
2) Bestimmen Sie die Umkehrfunktion von \( f \) und überprüfen Sie Ihre Antwort anhand einiger Punkte.
Lernen Sie, wie man mathematische Probleme mit Umkehrfunktionen sowohl mit analytischen Techniken als auch mit grafischen Methoden löst. Diese Seite bietet Schritt-für-Schritt-Lösungen zu einer Vielzahl von Fragen und hebt Schlüsselkonzepte wie die Spiegelungseigenschaft hervor: Der Graph einer Funktion und ihrer Umkehrfunktion sind Spiegelbilder entlang der Geraden \( y = x \). Ideal für Schüler und Lehrkräfte, die klare Erklärungen und ein visuelles Verständnis von Umkehrfunktionen suchen.
Unten ist der Graph von \[ f(x) = 2 x^3 - 1 \] dargestellt.
1) Zeichnen Sie den Graphen der Umkehrfunktion von \( f \) in dasselbe Koordinatensystem.
2) Bestimmen Sie die Umkehrfunktion von \( f \) und überprüfen Sie Ihre Antwort anhand einiger Punkte.
1) Punkte auf dem Graphen von \( f \) finden. Hier ist eine Liste von Punkten, deren Koordinaten \( (a , b) \) leicht aus dem Graphen bestimmt werden können: \[ (1 , 1), \quad (0 , -1), \quad (-1 , -3) \]
Auf dem Graphen der Umkehrfunktion haben die obigen Punkte die Koordinaten \( (b , a) \) wie folgt: \[ (1 , 1), \quad (-1 , 0), \quad (-3 , -1) \]
Zeichnen Sie die obigen Punkte und skizzieren Sie den Graphen der Umkehrfunktion von \( f \), sodass die beiden Graphen Spiegelungen voneinander an der Geraden \( y = x \) sind, wie unten gezeigt.
2) Schreiben Sie die gegebene Funktion \( f(x) = 2x^3 - 1 \) als Gleichung mit zwei Unbekannten: \[ y = 2x^3 - 1 \]
Lösen Sie die obige Gleichung nach \( x \) auf: \[ 2x^3 = y + 1 \] \[ x^3 = \dfrac{y + 1}{2} \] \[ x = \sqrt[3]{\dfrac{y + 1}{2}} \]
Vertauschen Sie \( x \) und \( y \) und schreiben Sie die Gleichung der Umkehrfunktion \( f^{-1} \): \[ y = \sqrt[3]{\dfrac{x + 1}{2}} \] \[ f^{-1} (x) = \sqrt[3]{\dfrac{x + 1}{2}} \]
Wir überprüfen nun, dass die Punkte \( \quad (1 , 1), \quad (-1 , 0), \quad (-3 , -1) \quad \), die oben zum Skizzieren des Graphen der Umkehrfunktion verwendet wurden, auf dem Graphen von \( f^{-1} \) liegen. \[ f^{-1} (1) = \sqrt[3]{\dfrac{1 + 1}{2}} = 1 \] \[ f^{-1} (-1) = \sqrt[3]{\dfrac{-1 + 1}{2}} = 0 \] \[ f^{-1} (-3) = \sqrt[3]{\dfrac{-3 + 1}{2}} = -1 \]
Sei \( f(x) = x^2 - 4x + 5 \), \( x \leq 2 \).
1) Finden Sie die Umkehrfunktion von \( f \).
2) Finden Sie die Definitionsmenge und die Wertemenge von \( f^{-1} \).
1) Wir haben eine quadratische Funktion mit einem eingeschränkten Definitionsbereich. Wir schreiben die gegebene Funktion zuerst in Scheitelpunktform (dies kann durch quadratische Ergänzung geschehen):
\[ f(x) = x^2 - 4x + 5 = (x - 2)^2 + 1, \quad x \leq 2 \]
Der Graph der Funktion \( f \) ist der der linken Hälfte einer Parabel mit Scheitelpunkt bei \( (2, 1) \), wie unten gezeigt.
Wir schreiben nun die gegebene Funktion als Gleichung. \[ y = (x - 2)^2 + 1 \]
Lösen Sie die obige Gleichung nach \( x \) auf. \[ y = (x - 2)^2 + 1 \] \[ (x - 2)^2 = y - 1 \]
Zwei Lösungen: \[ x - 2 = \pm \sqrt{y - 1} \] was ergibt \[ x = \sqrt{y - 1} + 2 \quad \text{und} \quad x = -\sqrt{y - 1} + 2 \]
Da \( x \leq 2 \) (Definitionsbereich von \( f \)) und \( \sqrt{y - 1} \ge 0 \), wählen wir die Lösung
\[ x = -\sqrt{y - 1} + 2 \]
Vertauschen Sie \( x \) und \( y \), um die Umkehrfunktion von \( f \) wie folgt zu schreiben. \[ y = f^{-1}(x) = -\sqrt{x - 1} + 2 \]
Die Definitionsmenge und Wertemenge von \( f^{-1} \) sind die Wertemenge und der Definitionsbereich von \( f \).
Definitionsmenge von \( f^{-1} \) ist die Wertemenge von \( f \): \[ [1, +\infty) \quad \text{(aus dem Graphen)} \]
Wertemenge von \( f^{-1} \) ist der Definitionsbereich von \( f \): \[ (-\infty, 2] \quad \text{(gegeben)} \]
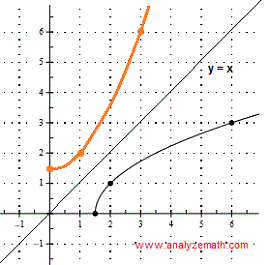
Unten ist der Graph von \[ f(x) = \sqrt{2 x - 3} \] dargestellt.
1) Skizzieren Sie die Umkehrfunktion von \( f \) im selben Graphen.
2) Finden Sie die Umkehrfunktion und überprüfen Sie Ihre Antwort anhand einiger Punkte.
1) Lokalisieren Sie einige Punkte auf dem Graphen von \( f \). Eine mögliche Liste von Punkten mit Koordinaten \( (a, b) \) ist wie folgt: \[ (1.5, 0) , (2, 1) , (6, 3) \]
Auf dem Graphen der Umkehrfunktion haben die obigen Punkte die Koordinaten \( (b, a) \) wie folgt: \[ (0, 1.5) , (1, 2) , (3, 6) \]
Zeichnen Sie die obigen Punkte und skizzieren Sie den Graphen der Umkehrfunktion von \( f \), sodass die beiden Graphen Spiegelungen voneinander an der Geraden \( y = x \) sind, wie unten gezeigt.
2) Schreiben Sie die gegebene Funktion \( f(x) = \sqrt{2x - 3} \) als Gleichung mit zwei Unbekannten. \[ y = \sqrt{2x - 3} \]
Lösen Sie die obige Gleichung nach \( x \) auf. Zuerst beide Seiten quadrieren: \[ 2x - 3 = y^2 \] \[ 2x = y^2 + 3 \] Lösen \[ x = \dfrac{y^2 + 3}{2} \]
Vertauschen Sie \( x \) und \( y \) und schreiben Sie die Gleichung der Umkehrfunktion \( f^{-1} \); und geben Sie die Definitionsmenge der Umkehrfunktion an. \[ y = \dfrac{x^2 + 3}{2} \] Die Definitionsmenge von \( f^{-1} \) ist die Wertemenge von \( f \) aus seinem Graphen oben, daher \[ f^{-1}(x) = \dfrac{x^2 + 3}{2}, \quad x \geq 0 \]
Wir überprüfen nun, dass die Punkte \( (0 , 1.5) \), \( (1 , 2) \) und \( (3 , 6) \), die zum Skizzieren des Graphen der Umkehrfunktion verwendet wurden, auf dem Graphen von \( f^{-1} \) liegen. \[ f^{-1}(0) = \dfrac{0^2 + 3}{2} = 1.5 \] \[ f^{-1}(1) = \dfrac{1^2 + 3}{2} = 2 \] \[ f^{-1}(3) = \dfrac{3^2 + 3}{2} = 6 \]
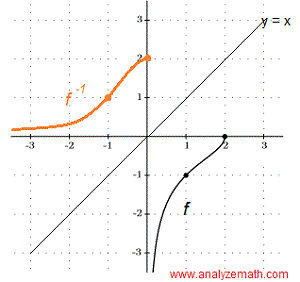
Skizzieren Sie den Graphen von \( f^{-1} \) mithilfe des unten gezeigten Graphen von \( y = f(x) \) und finden Sie \( f^{-1}(x) \).
1) Verwenden Sie den Graphen, um Punkte auf dem Graphen von \( f \) zu finden. Eine mögliche Liste von Punkten, deren Koordinaten \( (a , b) \) sind, ist wie folgt: \[ (0 , 3) , (2 , -1) , (5 , -3) \]
Auf dem Graphen der Umkehrfunktion haben die obigen Punkte die Koordinaten \( (b , a) \) wie folgt: \[ (3 , 0) , (-1 , 2) , (-3 , 5) \]
2) Bestimmung der Umkehrfunktion \( f^{-1}(x) \)
Für \( -3 \leq x \leq -1 \) ist \( f^{-1}(x) \) ein linearer Ausdruck mit der Steigung \( m_1 \), der durch die Punkte \( (-1, 2) \) und \( (-3, 5) \) verläuft:
\[ m_1 = \dfrac{5 - 2}{-3 - (-1)} = \dfrac{-3}{2} \]Daher gilt für \( -3 \leq x \leq -1 \) die Umkehrfunktion:
\[ f^{-1}(x) = -\dfrac{3}{2}(x - (-1)) + 2 = -\dfrac{3}{2}(x + 1) + 2 \]Für \( -1 < x \leq 3 \) ist \( f^{-1}(x) \) ein linearer Ausdruck mit der Steigung \( m_2 \), der durch die Punkte \( (-1, 2) \) und \( (3, 0) \) verläuft:
\[ m_2 = \dfrac{0 - 2}{3 - (-1)} = \dfrac{-2}{4} = -\dfrac{1}{2} \]Daher gilt für \( -1 < x \leq 3 \) die Umkehrfunktion:
\[ f^{-1}(x) = -\dfrac{1}{2}(x - (-1)) + 2 = -\dfrac{1}{2}(x + 1) + 2 \] Zusammenfassung: \[ f^{-1}(x) = \left \{ \begin{array}{ll} -\dfrac{3}{2}(x + 1) + 2 \quad -3 \leq x \leq -1 \\ -\dfrac{1}{2}(x + 1) + 2 \quad -1 \lt x \leq 3 \end{array} \right \} \] Die eineindeutige Funktion
\[ f(x) = - \sqrt{\dfrac{2}{x}-1} \]
ist unten grafisch dargestellt.
1) Was sind die Definitionsmenge und die Wertemenge von \( f \)?
2) Skizzieren Sie den Graphen von \( f^{-1} \).
3) Finden Sie \( f^{-1}(x) \) (inklusive Definitionsmenge).
1) \( f(x) \) ist als reelle Zahl definiert, wenn der Radikand \( \dfrac{2}{x} - 1 \) größer oder gleich 0 ist. Daher müssen wir die Ungleichung lösen:
\[
\dfrac{2}{x} - 1 \geq 0
\]
\[
\dfrac{2 - x}{x} \geq 0
\]
Der Ausdruck auf der linken Seite der Ungleichung wechselt sein Vorzeichen an den Nullstellen des Zählers und Nenners, die \( x = 2 \) und \( x = 0 \) sind. Siehe Tabelle unten.
Definitionsmenge von \( f \): \( (0 , 2] \)
Wertemenge von \( f \): \( (-\infty , 0] \)
2) Punkte auf dem Graphen von \( f \): \[ (2 , 0) , (1 , -1) \] Die obigen Punkte haben auf dem Graphen der Umkehrfunktion die Koordinaten \( (b , a) \) wie folgt: \[ (0 , 2) , (-1 , 1) \]
Zeichnen Sie die obigen Punkte und skizzieren Sie den Graphen der Umkehrfunktion von \( f \), sodass die beiden Graphen Spiegelungen voneinander an der Geraden \( y = x \) sind, wie unten gezeigt.
3) Schreiben Sie \( f(x) \) als Gleichung in \( y \) und \( x \). \[ y = -\sqrt{\dfrac{2}{x} - 1} \]
Lösen Sie die obige Gleichung nach \( x \) auf. Quadrieren Sie beide Seiten der obigen Gleichung: \[ y^2 = \dfrac{2}{x} - 1 \] \[ \dfrac{2}{x} = y^2 + 1 \] \[ x = \dfrac{2}{y^2 + 1} \]
Vertauschen Sie \( x \) und \( y \) und schreiben Sie die Umkehrfunktion: \[ y = \dfrac{2}{x^2 + 1} \] \[ f^{-1}(x) = \dfrac{2}{x^2 + 1} \]
Definitionsmenge und Wertemenge von \( f^{-1} \) sind die Wertemenge und der Definitionsbereich von \( f \). Daher:
Definitionsmenge von \( f^{-1} \): \[ (-\infty , 0] \]
Wertemenge von \( f^{-1} \): \[ (0 , 2] \]
Finden Sie die Umkehrfunktion von \[ f(x) = \log_4 (x + 2) - 5 \], sowie ihre Definitionsmenge und Wertemenge.
Schreiben Sie die gegebene Funktion als Gleichung in \( x \) und \( y \) wie folgt: \[ y = \log_{4}(x + 2) - 5 \]
Lösen Sie die obige Gleichung nach \( x \) auf. \[ \log_{4}(x + 2) = y + 5 \] \[ x + 2 = 4^{(y + 5)} \] \[ x = 4^{(y + 5)} - 2 \]
Vertauschen Sie \( x \) und \( y \). \[ y = 4^{(x + 5)} - 2 \]
Schreiben Sie die Umkehrfunktion mit ihrer Definitionsmenge und Wertemenge. \[ f^{-1}(x) = 4^{(x + 5)} - 2, \quad \text{Definitionsmenge: } (-\infty, +\infty), \quad \text{Wertemenge: } (-2, +\infty) \]
Wenn \( f(x) = \ln(x) + 4x - 8 \), was ist der Wert von \( f^{-1}(-4) \)?
Sei \( a = f^{-1}(-4) \). Dann schreiben wir unter Verwendung der Eigenschaft \( f(f^{-1}(x)) = x \) der Umkehrfunktion: \[ f(a) = f(f^{-1}(-4)) = -4 \]
Wir müssen nun ein \( a \) finden, so dass \( f(a) = -4 \), daher die zu lösende Gleichung:
\[ \ln(a) + 4a - 8 = -4 \] \[ \ln(a) = 4 - 4a \]
Die obige Gleichung kann nicht analytisch gelöst werden, aber ihre Lösung kann grafisch als die \( x \)-Koordinate des Schnittpunkts der Graphen von \( y = \ln(x) \) und \( y = 4 - 4x \) angenähert werden, wie unten gezeigt.
Der Schnittpunkt der beiden Graphen liegt nahe \( x = 1 \), von dem leicht überprüft werden kann, dass es die exakte Lösung der Gleichung \( \ln(x) = 4 - 4x \) ist. Daher gilt: \[ f^{-1}(-4) = 1 \]