Detaillierte Lösungen zu Fragen zu Skalar- und Kreuzprodukten von 3D-Vektoren.
1) Berechnen Sie \( \vec{u} \cdot (\vec{u} \times \vec{v}) \) unter der Annahme, dass \( \vec{u} = \lt a,b,c \gt \) und \( \vec{v} = \lt d,e,f \gt \).
Lösung
Das Vektorprodukt \( \vec{u} \times \vec{v}\) ist ein Vektor senkrecht zu beiden Vektoren \( \vec{u} \) und \( \vec{v} \). Daher ist das Skalarprodukt von zwei senkrechten Vektoren \( \vec{u} \) und \( \vec{u} \times \vec{v} \) gleich 0.
\( \vec{u} \cdot (\vec{u} \times \vec{v}) = 0 \)
2) Finden Sie \( k \) so, dass die Vektoren \( \vec{u} = \lt -2,-k,1 \gt \) und \( \vec{v} = \lt 8,-2,-3 > \) senkrecht sind.
Lösung
Wenn zwei Vektoren \( \vec{u} \) und \( \vec{v}\) senkrecht zueinander stehen, ist ihr Skalarprodukt gleich 0. Daher
\( \vec{u} \cdot \vec{v} = \lt -2,-k,1 \gt \cdot \lt 8,-2,-3> = 0 \)
Erweitern Sie das Skalarprodukt, um die Gleichung zu erhalten.
\( (-2)(8)+(-k)(-2)+(1)(-3) = 0 \)
Vereinfachen Sie und lösen Sie nach \( k \).
\( -16 + 2 k - 3 = 0 \)
\( k = 19/2 \)
3) Finden Sie \( k \), so dass die Vektoren \( \vec{u} = \lt -3,2,-2 \gt \), \( \vec{v} = \lt 2,1,k > \) und \( \vec{w} = \lt -1,3,-5 > \) in derselben Ebene liegen (oder koplanar sind)?
Lösung
Zwei Vektoren liegen in derselben Ebene (oder sind koplanar). Wenn ein dritter Vektor in dieser Ebene ist, ist das Volumen des Parallelepipeds (siehe Formel in Skalar- und Vektorprodukte von 3D-Vektoren) gebildet durch die 3 Vektoren gleich 0. Daher ist die Bedingung dafür, dass drei (nicht-null) Vektoren koplanar sind:
\( \vec{u} \cdot (\vec{v} \times \vec{w} ) = 0 \)
\( \vec{u} \cdot (\vec{v} \times \vec{w} ) \) wird als das skalare Tripelprodukt bezeichnet und ist gegeben durch:
\( \vec{u} \cdot (\vec{v} \times \vec{w} ) = \text{det} \begin{bmatrix}
u_x & u_y & u_z \\
v_x& v_y & v_z \\
w_x& w_y & w_z
\end{bmatrix} \)
wo \( u_x, u_y, u_z, v_x... \) die Komponenten der drei Vektoren sind.
Wir setzen jetzt die Komponenten ein und berechnen die Determinante.
\( \vec{u} \cdot (\vec{v} \times \vec{w} ) = \text{det} \begin{bmatrix}
-3 & 2 & -2 \\
2 & 1 & k \\
-1 & 3 & -5
\end{bmatrix} \) = -3(-5 - 3k) - 2(-10 +k) -2(6 + 1) = 21+7k
Damit die drei Vektoren in derselben Ebene liegen, muss die oben gefundene Determinante gleich null sein.
\( 21+7k = 0 \)
Lösen Sie die obige Gleichung nach \( k \), um zu erhalten:
\( k = -3 \)
Im Folgenden sind die drei Vektoren auf derselben Ebene dargestellt.
4) Finde den Winkel \( \theta \) zwischen den Vektoren \( \vec{u} = \lt 2,0,1 \gt \) und \( \vec{v} = \lt 8,-2,-3 > \).
Lösung
Verwende die Definition des Skalarprodukts von zwei Vektoren \( \vec{u} \) und \( \vec{v} \) und dessen Ausdruck unter Verwendung der Vektorkomponenten.
Definition: \( \vec{u} \cdot \vec{v} = ||\vec{u}|| || \vec{v} || \cos \theta \) , θ ist der Winkel zwischen den beiden Vektoren.
Das Skalarprodukt ist auch gegeben durch:
\( \vec{u} \cdot \vec{v} = u_x v_x + u_y v_y + u_z v_z \) , wobei \( u_x, v_x, u_y, ...\) die Komponenten der Vektoren \( \vec{u} \) und \( \vec{v} \) sind.
Berechnen wir nun die Beträge \( ||\vec{u}||\) und \( || \vec{v} || \) .
\( ||\vec{u}|| = \sqrt{2^2+0^2+1^2} = \sqrt{5} \)
\( ||\vec{v}|| = \sqrt{8^2+(-2)^2+(-3)^2} = \sqrt{77} \)
Jetzt verwenden wir die Komponenten, um das Skalarprodukt zu berechnen.
\( \vec{u} \cdot \vec{v} = (2)(8)+(0)(-2)+(1)(-3) = 13 \)
Jetzt verwenden wir die Definition, um den Winkel θ zu finden.
\( \vec{u} \cdot \vec{v} = ||\vec{u}|| || \vec{v} || \cos \theta \)
\( \cos \theta = \dfrac{\vec{u} \cdot \vec{v}}{||\vec{u}|| || \vec{v} ||} = \dfrac{13}{\sqrt{5}\sqrt{77}} \)
\( \theta = \arccos \dfrac{13}{\sqrt{5}\sqrt{77}} = 48,5^{\circ} \)
5) Finde die Vektorprojektion von \( \vec{u} = \lt -1,-1,1 \gt \) auf \( \vec{v} = \lt 2,1,1 > \).
Lösung
Die Vektorprojektion von \( \vec{u}\) auf \( \vec{v}\) wird durch (siehe Formel in Skalar- und Vektorprodukte von 3D-Vektoren) gegeben:
\( \text{proj}_{\vec{v}}\vec{u} = \dfrac{\vec{u}\cdot\vec{v}}{||v||^2} \vec{v} \)
\( = \dfrac{ \lt -1,-1,1 \gt \cdot \lt 2,1,1>}{2^2+1^2+1^2} \lt 2,1,1> = \dfrac{(-1)(2)+(-1)(1)+(1)(1)}{6} \lt 2,1,1 >\)
\( = -\dfrac{2}{6} \lt 2,1,1> = \lt -2/3,-1/3,-1/3> \)
Die Vektoren \( \vec{u}\) , \( \vec{v}\) und \( \text{proj}_{\vec{v}}\vec{u}\) sind unten dargestellt.
6) Finde \( k \) so, dass die Punkte \( A(-1,2,k) \), \( B(-3,6,3) \) und \( C(1,3,6) \) die Eckpunkte eines rechtwinkligen Dreiecks mit einem rechten Winkel bei \( A \) sind.
Lösung
Damit das Dreieck ABC bei A rechtwinklig ist, müssen die Vektoren \( \vec{AB} \) und \( \vec{AC}\) senkrecht zueinander stehen und daher ihr Skalarprodukt gleich null sein. Wir beginnen damit, die Komponenten der Vektoren zu berechnen.
\( \vec{AB} = \lt -2,4,3-k> \)
\( \vec{AC} = \lt 2,1,6-k> \)
Das Skalarprodukt von \( \vec{AB} \) und \( \vec{AC}\) muss null sein.
\( \lt -2,4,3-k> \cdot \lt 2,1,6-k > = 0 \)
\( -4 + 4 + (3-k)(6-k) = 0 \)
Vereinfachen und lösen Sie nach k auf.
Zwei Lösungen: \( k = 3 \) und \( k = 6 \)
7) Gegeben sei der Vektor \( \vec{v} = \lt 3,-1,-2 \gt \), finde den Vektor \( \vec{u} \) so, dass \( \vec{v} \times \vec{u} = \lt 4,2,5 > \) und \( ||\vec{u}|| = 3\)
Lösung
Seien a, b und c die Komponenten des Vektors \( \vec{u} \). Daher
\( \vec{v} \times \vec{u} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ 3 & -1 & -2 \\ a & b & c \end{vmatrix}} \)
\( = {\begin{vmatrix} -1 & -2 \\ b & c \end{vmatrix}} \vec{i} - {\begin{vmatrix}3 & -2\\ a & c\end{vmatrix}} \vec{j} + {\begin{vmatrix}3 & -1\\ a& b\end{vmatrix}} \vec{k} = (-c+2b)\vec{i} + (-2a-3c)\vec{j} + (3b+a)\vec{k} \)
Wir setzen nun die Komponenten von \( \vec{v} \times \vec{u} \) gleich den gegebenen \( \lt 4,2,5 > \) oben. Daher
\( -c+2b = 4 \)
\( -2a-3c = 2 \)
\( 3b+a = 5 \)
Beachten Sie, dass die Gleichungen im obigen System nicht unabhängig sind (addieren Sie -3 mal die erste Gleichung -c+2b = 4 und die zweite Gleichung -2a-3c = 2, und Sie erhalten eine Gleichung, die der dritten Gleichung 3b+a = 5 entspricht), und es hat daher viele Lösungen. Setzen Sie a = t und verwenden Sie die zweite Gleichung, um c zu finden.
-2t - 3c = 2
c = (2 + 2t) / (-3)
Setzen Sie a erneut auf t und verwenden Sie die dritte Gleichung, um b zu finden.
3b + t = 5
b = (5 - t) / 3
Wir verwenden nun die Bedingung \( ||\vec{u}|| = 3\) um die Gleichung zu schreiben.
\( \sqrt{a^2+b^2+c^2} = 3 \)
Beide Seiten der obigen Gleichung quadrieren und a, b und c durch ihre Ausdrücke in Bezug auf t ersetzen.
\( t^2+((5 - t) / 3)^2+((2 + 2t) / (-3))^2 = 9 \)
Multiplizieren Sie alle Terme der Gleichung mit 9 und vereinfachen Sie.
\( 9 t^2+(5 - t)^2+(2 + 2t)^2 = 81 \)
Erweitern Sie die obige Gleichung, um eine quadratische Gleichung zu erhalten, und lösen Sie sie, um
t = 2 und t = -13/7
Daher zwei Lösungen für den Vektor \( \vec{u} \).
für t = 2: \( \vec{u_1} = \lt t , (5 - t)/3 , (2 + 2t)/(-3) > = \lt 2 , 1, -2 > \)
für t = -13/7: \( \vec{u_2} = \lt t , (5 - t)/3 , (2 + 2t)/(-3) > = \lt -13/7 , 16/7 , 4/7> \)
8) Die Punkte A, B, C und D bilden ein Parallelogramm.
a) Finde die Koordinaten des Punktes D.
b) Finde die Fläche des Parallelogramms.
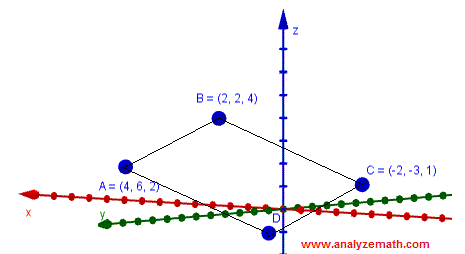
Lösung
a) Seien a, b und c die Koordinaten des Punktes D und bestimme die Komponenten der Vektoren \( \vec{AB} \) und \( \vec{DC} \).
\( \vec{AB} = \lt 2 - 4 , 2 - 6 , 4 - 2 > = \lt -2 ,-4 ,2> \)
\( \vec{DC} = \lt -2 - a , -3 - b , 1 - c> \)
Damit A, B, C und D ein Parallelogramm bilden, müssen die Vektoren \( \vec{AB} \) und \( \vec{DC} \) gleich sein. Daher die Vektorgleichung
\( \lt -2 , -4 , 2 > = \lt -2 - a , -3 - b , 1 - c> \)
Die uns 3 algebraische Gleichungen gibt.
-2 - a = -2
-3 - b = -4
1 - c = 2
Die die Koordinaten des Punktes D ergibt.
D(0, 1 , -1)
b) Die Fläche A des Parallelogramms ist gegeben durch (siehe Formel in Skalar- und Vektorprodukte von 3D-Vektoren)
A = \( || \vec{AB} \times \vec{BC} || \)
Berechnen wir zuerst das Vektorprodukt,
\( \vec{AB} \times \vec{BC} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ -2 & -4 & 2 \\ -4 & -5 & -3 \end{vmatrix}} = {\begin{vmatrix} -4 & 2 \\ -5 & -3 \end{vmatrix}} \vec{i} - {\begin{vmatrix}-2 & 2\\ -4 & -3\end{vmatrix}} \vec{j} + {\begin{vmatrix}-2 & -4\\ -4& -5\end{vmatrix}} \vec{k} = 22\vec{i} + 14\vec{j} -6\vec{k} \)
dann seinen Betrag, der die Fläche A ist.
A = \( ||\vec{AB} \times \vec{BC}|| = \sqrt{22^2+14^2+(-6)^2} = 2\sqrt{179} \)
9) In dem unten stehenden Würfel finde den Winkel zwischen den Diagonalen AG und BH.
Lösung
Zuerst finden wir die Komponenten der Vektoren \( \vec{AG}\) und \( \vec{BH} \).
\( \vec{AG} = \lt 2,2,2>\)
\( \vec{BH} = \lt -2,2,2> \)
Unter Verwendung des Skalarprodukts, wobei θ der Winkel zwischen den Vektoren \( \vec{AG}\) und \( \vec{BH} \) ist, haben wir (siehe Frage 5 oben).
\( \cos \theta = \dfrac{\vec{AG} \cdot \vec{BG}}{||\vec{AG}|| || \vec{BH} ||} = \dfrac{2\cdot (-2)+2\cdot2+2\cdot2}{\sqrt{2^2+2^2+2^2}\sqrt{(-2)^2+2^2+2^2}} = \dfrac{1}{3}\)
\( \theta = \arccos \dfrac{1}{3} \approx 70.5^{\circ} \)
10) Finde einen Vektor, der orthogonal zur Ebene ist, die die Punkte A(1,2,-3), B(0,-2,1) und C(-2,0,1) enthält.
Lösung
Ein Vektor \( \vec{v} \), der orthogonal zur oben definierten Ebene ist, könnte durch das Kreuzprodukt von zwei verschiedenen Vektoren in der Ebene gegeben sein. Daher.
\( \vec{v} = \vec{AB} \times \vec{AC} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ -1 & -4 & 4 \\ -3 & -2 & 4 \end{vmatrix}} = {\begin{vmatrix} -4 & 4 \\ -2 & 4 \end{vmatrix}} \vec{i} - {\begin{vmatrix}-1 & 4\\ -3 & 4\end{vmatrix}} \vec{j} + {\begin{vmatrix}-1 & -4\\ -3& -2\end{vmatrix}} \vec{k} = -8\vec{i} - 8\vec{j} -10\vec{k} \)
Beachte, dass es eine unendliche Anzahl von Lösungen gibt.
11) Berechne die Fläche des Dreiecks mit den Eckpunkten A(1,0,-3), B(1,-2,0) und C(0,2,1).
Lösung
Die Fläche \( A_t \) eines Dreiecks wird durch die Hälfte des Betrags des Kreuzprodukts von zwei Vektoren, die die Seiten des Dreiecks bilden, gegeben. Daher
\( A_t = \vec{AB} \times \vec{AC} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ 0 & -2 & 3 \\ -1 & 2 & 4 \end{vmatrix}} = {\begin{vmatrix} -2 & 3 \\ 2 & 4 \end{vmatrix}} \vec{i} - {\begin{vmatrix}0 & 3\\ -1 & 4\end{vmatrix}} \vec{j} + {\begin{vmatrix}0 & -2\\ -1& 2\end{vmatrix}} \vec{k} = -14\vec{i} - 3\vec{j} -2\vec{k} \)
\( A_t = (1/2) || \vec{AB} \times \vec{AC} || = \sqrt{(-14)^2 + (-3)^2 + (-2)^2} = (1/2) \sqrt{209} \) Einheit2
12) Berechne das Volumen des unten gezeigten Parallelepipeds.
