Wir beginnen mit der linken Seite der gegebenen Identität.

Verwenden Sie die Identität \( \tan(x) = \dfrac{\sin(x)}{\cos(x)} \) auf der linken Seite der gegebenen Identität, um zu schreiben: \[ \tan^2(x) - \sin^2(x) = \left(\dfrac{\sin(x)}{\cos(x)}\right)^2 - \sin^2(x) \] \[ = \dfrac{\sin^2(x)}{\cos^2(x)} - \sin^2(x) \] \[ = \dfrac{\sin^2(x) - \cos^2(x) \sin^2(x)}{\cos^2(x)} \] \[ = \dfrac{\sin^2(x) \left(1 - \cos^2(x)\right)}{\cos^2(x)} \] \[ = \dfrac{ \sin^2(x) \sin^2(x)}{\cos^2(x)} \] \[ = \sin^2(x) \tan^2(x) \] was der rechten Seite der gegebenen Identität entspricht.

Verwenden Sie die Identitäten \( \cos(2x) = 2 \cos^2(x) - 1 \) und \( \sin(2x) = 2 \sin(x) \cos(x) \) auf der linken Seite der gegebenen Identität, um zu schreiben: \[ \dfrac{1 + \cos(x) + \cos(2x)}{\sin(x) + \sin(2x)} \] \[ = \dfrac{1 + \cos(x) + 2 \cos^2(x) - 1}{\sin(x) + 2 \sin(x) \cos(x) } \] \[ = \dfrac{\cos(x) + 2 \cos^2(x)}{\sin(x) + 2 \sin(x) \cos(x) } \] \[ = \dfrac{\cos(x) (1 + 2 \cos(x))}{\sin(x) (1 + 2 \cos(x)) } \] \[ = \dfrac{\cos(x)}{\sin(x)} \] \[ = \cot(x) \] was der rechten Seite der gegebenen Identität entspricht.

Verwenden Sie die Identität \( \sin(2x) = 2 \sin(x) \cos(x) \), um \( \sin(4x) = 2 \sin(2x) \cos(2x) \) auf der rechten Seite der gegebenen Identität zu schreiben: \[ \dfrac{\sin(4x)}{\cos(2x)} = \dfrac{2 \sin(2x) \cos(2x)}{\cos(2x)}\] \[ = 2 \sin(2x) \] \[ = 2 \times 2 \sin(x) \cos(x) \] \[ = 4 \sin(x) \cos(x) \] was der linken Seite der gegebenen Identität entspricht.

Verwenden Sie die Identität \( \sin(2x) = 2 \sin(x) \cos(x) \), um \( \sin(x) \) zu schreiben als \[ \sin(x) = \sin(2 ( x/2 ) ) = 2 \sin(x / 2) \cos(x / 2) \] und setzen Sie es in die rechte Seite der gegebenen Gleichung ein, um sie wie folgt zu schreiben: \[ 2 \sin(x / 2) \cos(x / 2) + \sin(x / 2) = 0 \] Faktorisieren Sie \( \sin(x / 2) \)
\[ \sin(x/2) ( 2 \cos(x/2) + 1 ) = 0 \] was zwei zu lösende Gleichungen ergibt: \[ \sin(x/2) = 0 \quad \text{und} \quad 2 \cos(x/2) + 1 = 0 \] a) Die Gleichung \( \sin(x / 2) = 0 \) hat die Lösungen \( x / 2 = 0 \) und \( x / 2 = \pi \)

Lösen Sie nach \( x \) auf, um die Lösungen zu erhalten: \( x = 0 \) und \( x = 2 \pi \)

b) Die Gleichung \( 2 \cos(x/2) + 1 = 0 \) kann geschrieben werden als: \[ \cos(x/2) = -1/2 \] welches die Lösungen \( x/2 = 2 \pi/3 \) und \( x/2 = 4 \pi/3 \) hat.

Lösen Sie nach \( x \) auf, um die Lösungen zu erhalten: \( x = 4 \pi/3 \) und \( x = 8 \pi/3 \)

Beachten Sie, dass \( 8 \pi/3 \) größer als \( 2 \pi \) ist und daher nicht akzeptiert wird.

Endgültige Lösungen für die gegebene Gleichung sind: \( \{ 0 , 4 \pi/3 , 2 \pi \} \)

Die gegebene Gleichung ist bereits in faktorisierter Form: \[ (2\sin(x) - 1)(\tan(x) - 1) = 0 \] was zu zwei zu lösenden Gleichungen führt: \[ 2\sin(x) - 1 = 0 \quad \text{und} \quad \tan(x) - 1 = 0 \] Die obigen Gleichungen können geschrieben werden als: \[ \sin(x) = 1/2 \quad \text{und} \quad \tan(x) = 1 \] Die Lösungen der Gleichung \( \sin(x) = 1/2 \) sind: \[ x = \pi/6 \quad \text{und} \quad x = 5 \pi/6 \] Die Lösungen der Gleichung \( \tan(x) = 1 \) sind: \[ x = \pi /4 \quad \text{und} \quad x = 5 \pi/4 \] Die Lösungen der gegebenen Gleichung innerhalb des gegebenen Intervalls sind: \[ \{\pi/6, 5 \pi/6 , \pi /4 , 5 \pi/4 \} \]

Verwenden Sie die Formel für \( \cos(A + B) \), um zu schreiben: \[ \cos(3x) = \cos(2x + x) = \cos(2x) \cos(x) - \sin(2x) \sin(x) \] . Daher kann die gegebene Gleichung \[ \cos(2x) \cos(x) - \sin(2x) \sin(x) = 0 \] geschrieben werden als: \[ \cos(3x) = 0 \] Lösen Sie die obige Gleichung für \( 3x \) auf, um zu erhalten: \[ 3x = \pi/2 \quad \text{,} \quad 3x = 3\pi/2 \quad \text{,} \quad 3x = 5\pi/2 \quad \text{,} \quad 3x = 7\pi/2 \quad \text{,} \quad 3x = 9\pi/2 \quad \text{und} \quad 3x = 11\pi/2 \] Lösen Sie das Obige für \( x \) auf, um die Lösungen zu erhalten: \[ \{\pi/6, \pi/2, 5\pi/6, 7\pi/6, 3\pi/2 , 11\pi/6 \} \]

Verwenden Sie die Identitäten \( \sin(2x) = 2 \sin(x) \cos(x) \) und \( \cos(2x) = 1 - 2 \sin^2(x) \), um den gegebenen Ausdruck wie folgt umzuschreiben: \[ \dfrac{\sin(2x) - \cos(x)}{\cos(2x) + \sin(x) - 1 } = \dfrac{ 2 \sin(x) \cos(x) - \cos(x)}{1 - 2 \sin^2(x) + \sin(x) - 1 } \] Vereinfachen Sie die rechte Seite und faktorisieren Sie Zähler und Nenner: \[ = \dfrac{\cos(x)( 2 \sin(x) -1) }{ \sin(x)( - 2 \sin(x) + 1) } \] Vereinfachen Sie: \[ = - \dfrac{\cos(x)}{ \sin(x)} \] \[ = - \cot(x) \]

\( 105^{\circ} \) kann als Summe zweier besonderer Winkel wie folgt geschrieben werden: \[ 105^{\circ} = 60^{\circ} + 45^{\circ}\] Daher: \[ \sin(105^{\circ}) = \sin(60^{\circ} + 45^{\circ}) \] Verwenden Sie die Identitäten \( \sin(a + b) = \sin(a)\cos(b) + \cos(a)\sin(b) \), um zu schreiben: \[ \sin(105^{\circ}) = \sin(60^{\circ})\cos(45^{\circ}) + \cos(60^{\circ}) \sin(45^{\circ}) \] Verwenden Sie die Tabelle der besonderen Winkel: \[ = (\sqrt {3} / 2 )(\sqrt {2}/2) + (1/2)(\sqrt {2}/2) \] \[ = \dfrac{ \sqrt {6} + \sqrt {2} } {4} \]

Wenn \( \sin(x) = 2/5 \) dann ist \( \cos(x) = \sqrt {1 - \sin^2 x} = \sqrt{1 - (2/5)^2} = \sqrt{21}/5 \)

1. ) Verwenden Sie die Identität: \( \cos(2x) = 1 - 2 \sin^2(x) = 17/25 \)
2. ) Verwenden Sie die Identität: \[ \cos(4x) = 1 - 2 \sin^2(2 x) \] \[ = 1 - 2 [ 2\sin(x) \cos(x) ]^2 \] \[ = 457 / 625 \]
3. ) Verwenden Sie die Identität: \[ \sin(2x) = 2 \sin(x) \cos(x) = 4 \sqrt{21}/25 \]
4. ) Verwenden Sie die Identität: \[ \sin(4x) = \sin(2(2x)) = 2 \cos(2x) \sin(2x) \] \[ = 2 (17/25)(4 \sqrt{21}/25) = 136 \sqrt{21} / 625 \]

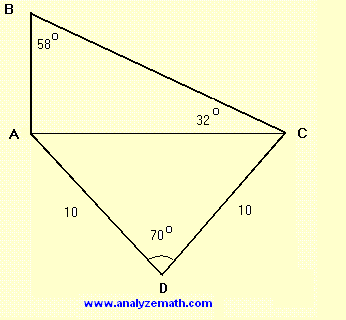Beachten Sie, dass das Dreieck \( DAC \) gleichschenklig ist. Wenn wir daher das Lot von D auf AC zeichnen, wird es AC in zwei Hälften teilen und den Winkel D halbieren. Daher:

. Daher können wir unter Verwendung des rechtwinkligen Dreiecks mit der Hypotenuse AD schreiben: \[ (1/2) AC = 10 \sin(35^{\circ}) \] was ergibt: \[ AC = 20 \sin(35^{\circ}) \] Beachten Sie, dass die beiden Innenwinkel B und C des Dreiecks ABC zusammen \( 90^{\circ} \) ergeben und daher der dritte Winkel des Dreiecks ABC ein rechter Winkel ist. Wir können daher schreiben: \[ \tan(32^{\circ}) = AB / AC \] Daraus ergibt sich: \[ AB = AC \tan(32^{\circ}) \] \[ = 20 \sin(35^{\circ})\tan(32^{\circ}) \approx 7.17 \quad \text{(gerundet auf 3 signifikante Stellen)} \]