Geometry Problems with Answers and Solutions - Grade 10

Grade 10 geometry problems with solutions are presented.

Problems

1. Each side of the square pyramid shown below measures 10 inches. The slant height, H, of this pyramid measures 12 inches.
   

   .
   

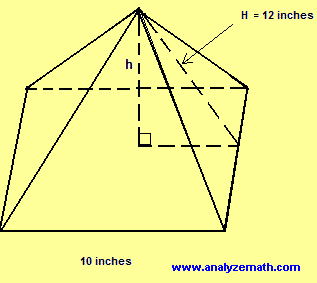
   1. What is the area, in square inches, of the base of the pyramid?
      
   2. What is the total surface area, in square inches, of the pyramid?
      
   3. What is h, the height, in inches, of the pyramid?
      
   4. Using the height you determined in part (c), what is the volume, in cubic inches, of the pyramid?
   
   
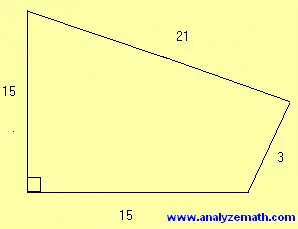2. The parallelogram shown in the figure below has a perimeter of 44 cm and an area of 64 cm². Find angle T in degrees.
   

   .
   

3. Find the area of the quadrilateral shown in the figure.(NOTE: figure not drawn to scale)
   

   .
   

4. In the figure below triangle OAB has an area of 72 and triangle ODC has an area of 288. Find x and y.
   

   .
   

5. Find the dimensions of the rectangle that has a length 3 meters more that its width and a perimeter equal in value to its area?
   
6. Find the circumference of a circular disk whose area is 100 π square centimeters.
   
7. The semicircle of area 1250 π centimeters is inscribed inside a rectangle. The diameter of the semicircle coincides with the length of the rectangle. Find the area of the rectangle.

Solutions to the Above Problems

1. 
   a) 100 inches squared
   b) 100 + 4×(1/2)×12×10 = 340 inches squared
   c) h = √(12² - 5²) = √(119)
   d) Volume = (1/3)×100×√(119)
   = 363.6 inches cubed (approximated to 4 decimal digits)
2. 
   

   

   
   44 = 2(3x + 2) + 2(5x + 4) , solve for x
   x = 2
   height = area / base
   = 64 / 14 = 32/7 cm
   sin(T) = Opp/ Hyp = (32/7) / 8 = 32/56 = 4/7
   T = arcsin(4/7) = 34.8^o
3. 
   

   

   
   ABD is a right triangle; hence BD² = 15² + 15² = 450
   Also BC² + CD² = 21² + 3² = 450
   The above means that triangle BCD is also a right triangle and the total area of the quadrilateral is the sum of the areas of the two right triangles.
   Area of quadrilateral = (1/2)×15×15 + (1/2)×21×3 = 144
4. 
   area of OAB = 72 = (1/2) sin (AOB) × OA × OB
   solve the above for sin(AOB) to find sin(AOB) = 1/2
   area of ODC = 288 = (1/2) sin (DOC) × OD × OD
   Note that sin(DOC) = sin(AOB) = 1/2, OD = 18 + y and OC = 16 + x and substitute in the above to obtain the first equation in x and y
   1152 = (18 + y)(16 + x)
   We now use the theorem of the intersecting lines outside a circle to write a second equation in x and y
   16 × (16 + x) = 14 × (14 + y)
   Solve the two equations simultaneously to obtain
   x = 20 and y = 14
5. 
   Let L be the length and W be the width of the rectangle. L = W + 3
   Perimeter = 2L + 2W = 2(W + 3) + 2W = 4W + 6
   Area = L W = (W + 3) W = W² + 3 W
   Area and perimeter are equal in value; hence
   W² + 3 W = 4W + 6
   Solve the above quadratic equation for W and substitute to find L
   W = 3 and L + 6
6. 
   Let r be the radius of the disk. Area is known and equal to 100π; hence
   100π = π r²
   Solve for r: r = 10
   Circumference = 2 π r = 20 π
7. 
   Let r be the radius of the semicircle. Area of the semicircle is known; hence
   1250π = (1/2) π r² (note the 1/2 because of the semicircle)
   Solve for r: r = 50
   Length of rectangle = 2r = 100 (semicircle inscribed)
   Width of rectangle = r = 50 (semicircle inscribed)
   Area = 100 × 50 = 5000

Links and References