Grade 10 Trigonometry Word Problems with Step-by-Step Solutions

\[ x = \frac{10}{\tan(51^\circ)} = 8.1 \; \text{ (2 significant digits)} \] \[ H = \frac{10}{\sin(51^\circ)} = 13 \; \text{ (2 significant digits) } \]

Area is given by: \[ \frac{1}{2}(2x)(x) = 400 \] Solve for x: \[ x = 20, \quad 2x = 40 \] Use Pythagoras' theorem: \[ (2x)^2 + (x)^2 = H^2 \] Solve for \( H \). \[ H = x \sqrt{5} = 20 \sqrt{5} \]

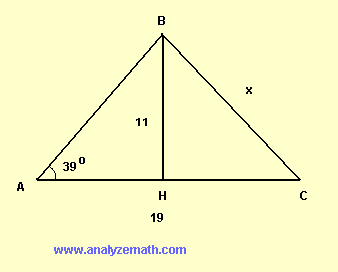
BH perpendicular to AC means that triangles \( \triangle ABH \) and \( \triangle HBC \) are right triangles. Hence: \[ \tan(39^\circ) = \frac{11}{AH} \quad \Rightarrow \quad AH = \frac{11}{\tan(39^\circ)} \] \[ HC = 19 - AH = 19 - \frac{11}{\tan(39^\circ)} \] Apply the Pythagorean theorem to triangle \( \triangle HBC \): \[ \quad 11^2 + HC^2 = x^2 \] Substitute HC and solve for \( x \). \[ x = \sqrt{11^2 + \left(19 - \frac{11}{\tan(39^\circ)}\right)^2} \] \[ x \approx 12.3 \quad \text{(rounded to 3 significant digits)} \]

Since \( \angle A \) is right, both triangles \( \triangle ABC \) and \( \triangle ABD \) are right, and therefore we can apply the Pythagorean theorem. \[ 14^2 = 10^2 + AD^2, \quad 16^2 = 10^2 + AC^2 \] Solve for AD and AC: \[ AD = \sqrt{14^2-10^2} , \quad AC = \sqrt{16^2 - 10^2} \] \[ \text{Also, } x = AC - AD \] \[ x = \sqrt{16^2 - 10^2} - \sqrt{14^2 - 10^2} \] \[ x \approx 2.69 \quad \text{(rounded to 3 significant digits)} \]

Use right triangle \(\triangle ABC\) to write: \[ \tan(31^\circ) = \frac{6}{BC} \quad \Rightarrow \quad BC = \frac{6}{\tan(31^\circ)} \] Use the Pythagorean theorem in the right triangle \triangle BCD to write: \[ 9^2 + BC^2 = BD^2 \] \text{Solve for } BD \text{ and substitute } BC: \[ BD = \sqrt{9^2 + \left( \frac{6}{\tan(31^\circ)} \right)^2} \] \[ BD \approx 13.4 \quad \text{(rounded to 3 significant digits)} \]

The triangle is right and one of its angles is \( 45^\circ \). The third angle is also \( 45^\circ \), and therefore the triangle is right and isosceles.

Let \( x \) be the length of one of the legs, and \( H \) be the hypotenuse. \[ \text{Area} = \frac{1}{2}x^2 = 50 \quad \Rightarrow \quad x = 10 \] Use the Pythagorean theorem: \[ \quad x^2 + x^2 = H^2 \] \[ \Rightarrow \quad H = 10\sqrt{2} \]

Let \( a \) be the length of the side opposite angle \( A \), \( b \) the length of the side adjacent to angle \( A \) and \( h \) the length of the hypotenuse. \[ \tan(A) = \frac{\text{opposite side}}{\text{adjacent side}} = \frac{a}{b} = \frac{3}{4} \] We can write that: \( a = 3k \) and \( b = 4k \) , where \( k \) is a coefficient of proportionality. Let us find \( h \). Using the Pythagorean theorem, we write: \[ \quad h^2 = (3k)^2 + (4k)^2 \] \[ h^2 = 9k^2 + 16k^2 = 25k^2 \quad \Rightarrow \quad h = 5k \] \[ \sin(A) = \frac{a}{h} = \frac{3k}{5k} = \frac{3}{5}, \quad \cos(A) = \frac{b}{h} = \frac{4k}{5k} = \frac{4}{5} \]

Let \( b \) be the length of the side opposite angle \( B \). \( c \) the length of the side opposite angle \( C \), and \( h \) the hypotenuse. \[ \sin(B) = \frac{b}{h}, \quad \cos(B) = \frac{c}{h} \] \[ \sin(B) = \cos(B) \quad \Rightarrow \quad \frac{b}{h} = \frac{c}{h} \quad \Rightarrow \quad b = c \] Since the two sides are equal in length, the triangle is isosceles, and angles \( B \) and \( C \) are equal, each measuring \( 45^\circ\).

The diagram below shows a rectangle with diagonals and half of one of the angles labeled \( x \).

\[ \tan(x) = \frac{5}{2.5} = 2 \quad \Rightarrow \quad x = \arctan(2) \] Larger angle made by diagonals is \( 2x \): \[ 2x = 2 \arctan(2) \approx 127^\circ \quad \text{(3 significant digits)} \] \[ \text{Smaller angle made by diagonals: } 180^\circ - 2x \approx 53^\circ \]

Let \( x \) be the length of side AC. Use the cosine law \[ 12^2 = 8^2 + x^2 - 2 \cdot 8 \cdot x \cdot \cos(59^\circ) \] Solve the quadratic equation for \( x \): \[ x = 14.0 \quad \text{and} \quad x = -5.7 \] Since \( x \) cannot be negative, the solution is: \[ x = 14.0 \quad \text{(rounded to one decimal place)} \]

\[ \tan(20^\circ) = \frac{200}{L} \] \[ L = \frac{200}{\tan(20^\circ)} \] \[ \tan(10^\circ) = \frac{H_2}{L} \] \[ H_2 = L \cdot \tan(10^\circ) \] \[ = \frac{200 \cdot \tan(10^\circ)}{\tan(20^\circ)} \] \[ \text{Height of second building} = 200 + H_2 = = 200 + \frac{200 \cdot \tan(10^\circ)}{\tan(20^\circ)} \approx 297 \text{ meters} \]

Let \( h \) be the initial height of the balloon above point \( P \). After rising, the new height is \( h + 50 \) meters.

The horizontal distance from the car to \( P \) is \( d \) (which remains constant).
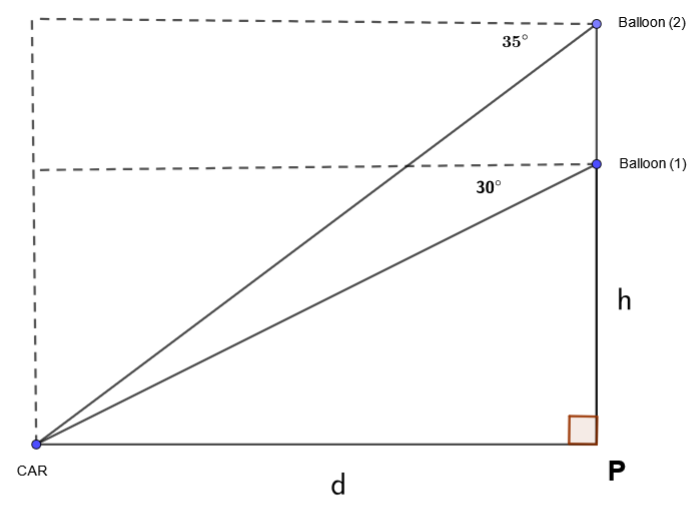
The angle of depression from the balloon to the car is equal to the angle of elevation from the car to the balloon (by alternate interior angles).
So, for the initial position: \[ \tan(30^\circ) = \frac{h}{d} \] \[ \frac{1}{\sqrt{3}} = \frac{h}{d} \quad \text{(since } \tan 30^\circ = \frac{1}{\sqrt{3}} \text{)} \] Thus, \[ h = \frac{d}{\sqrt{3}} \tag{1} \] After rising 50 meters, the new height is \( h + 50 \), and the angle of depression is \( 35^\circ \): \[ \tan(35^\circ) = \frac{h + 50}{d} \] So, \[ h + 50 = d \cdot \tan(35^\circ) \tag{2} \] Now substitute equation (1) into equation (2): \[ \frac{d}{\sqrt{3}} + 50 = d \cdot \tan(35^\circ) \] Rearrange to solve for \( d \): \[ 50 = d \cdot \tan(35^\circ) - \frac{d}{\sqrt{3}} \] \[ 50 = d \left( \tan(35^\circ) - \frac{1}{\sqrt{3}} \right) \] \[ d = \frac{50}{\tan(35^\circ) - \frac{1}{\sqrt{3}}} \] Use the numerical values: \( \tan(35^\circ) \approx 0.7002 \) and \( \frac{1}{\sqrt{3}} \approx 0.57735 \) to obtain: \[ d = \frac{50}{0.7002 - 0.57735} = \frac{50}{0.12285} \approx 406.97 \] Therefore, the car is approximately \( 407 \) meters from point \( P \).

Let \(h\) be the height of the building. Initially, when the angle of elevation is \(70^\circ\), the length of the shadow is \(s\).

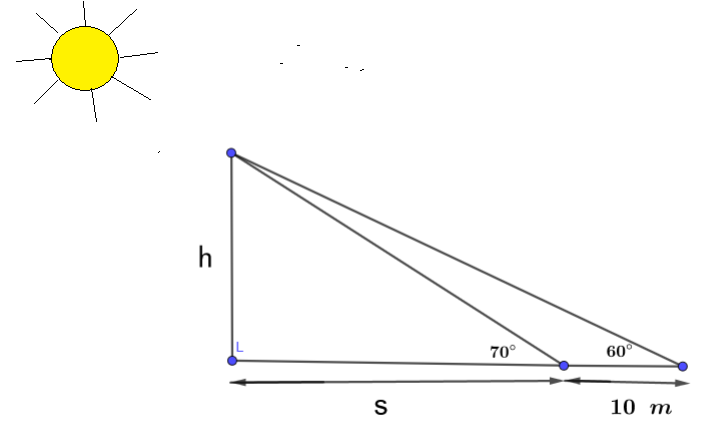
When the angle of elevation decreases to \(60^\circ\), the shadow length becomes \(s + 10\).
For the initial case (angle \(70^\circ\)): \[ \tan(70^\circ) = \frac{h}{s} \] So, \[ s = \frac{h}{\tan(70^\circ)} \tag{1} \] For the new case (angle \(60^\circ\)): \[ \tan(60^\circ) = \frac{h}{s + 10} \] So, \[ s + 10 = \frac{h}{\tan(60^\circ)} \tag{2} \] Now, subtract equation (1) from equation (2): \[ (s + 10) - s = \frac{h}{\tan(60^\circ)} - \frac{h}{\tan(70^\circ)} \] \[ 10 = h \left( \frac{1}{\tan(60^\circ)} - \frac{1}{\tan(70^\circ)} \right) \] So, \[ h = \frac{10}{ \frac{1}{\tan(60^\circ)} - \frac{1}{\tan(70^\circ)} } \] Simplify the expression: \[ h = \frac{10}{ \cot(60^\circ) - \cot(70^\circ) } \] Evaluate numerically: \[ h = \approx 46.86474 \] Therefore, the height of the building is approximately \(46.9\) meters.