Domain of a Square Root Function

How to find the domain of square root functions? Several examples are presented along with detailed solutions and explanations with graphical explanations and interpretation of the domain.

Find the Domain of a Square Root Function

We first need to understand that \( \sqrt x \) is real only if the argument \( x \) which is the quantity under the radical \( \sqrt{} \) satisfies the condition: \( x \ge 0 \). This can easily be verified by examining the graph of \( y = \sqrt x \) shown below: The graph exists only for \( x \ge 0 \).

graph of square root function

Examples with their Solutions

Example 1
Find the domain of the function \( f(x) = \sqrt{x - 2} \).
Solution:

\( f(x) = \sqrt{x - 2} \) takes real values if the argument \( x - 2 \), which is the quantity under the radical \( \sqrt{} \), satifies the condition: \( x - 2 \ge 0 \). The solution of the inequality is
\( x \ge 2 \)
which is the domain of the function and this can be checked graphically as shown below where the graph of \( f\) "exists" for \( x \ge 2 \).

graph of square root function in example 1

Example 2
Find the domain of the function \( f(x) = \sqrt{|x - 1|} \).
Solution

\( f(x) = \sqrt{|x - 1|} \) takes real values if the argument \( |x - 1| \), which is the quantity under the radical \( \sqrt{} \), satifies the condition: \( |x - 1| \ge 0 \). The solution of the inequality is
all real number because the absolute value expression \( |x - 1| \) is always positive or zero for \( x = 1 \).
The domain of the function is the set of real numbers \( \mathbb{R} \) and this can be checked graphically as shown below where the graph of \( f\) "exists" for all \( x \) values.

graph of square root function in example 2

Example 3
Find the domain of the function \( f(x) = \dfrac{1}{ \sqrt{x + 3}} \).
Solution
Taking into account that the function is the ratio of two functions and that division by zero is not allowed, the given function takes real values if the argument \( x + 3 \), which is the quantity under the radical \( \sqrt{} \), satisfies the condition: \( x + 3 \gt 0 \). Note the symbol of the inequality used is \( \gt \) and not \( \ge \) because we do not want to have zero in the denominator. Solution of the inequality is
\( x \gt - 3 \).
The domain of the function is the set of real numbers greater than -3 and this can be checked graphically as shown below where the graph of \( f\) "exists" for all \( x > - 3\) values.

graph of square root function in example 3

Example 4
Find the domain of the function \( f(x) = \dfrac{\sqrt{x + 4}}{ \sqrt{x - 2}} \).
Solution
The given function takes real values if two conditions are satisfied.
1) \( x + 4 \ge 0 \) , zero is allowed in the numerator, hence the use of the inequality symbol \( \ge \).
and
2) \( x - 2 \gt 0 \) , zero is not allowed in the denominator, hence the use of the inequality symbol \( \gt \).
The domain of the function is the intersection of the two solution sets of the two inequalities above.
\( x \ge - 4 \) and \( x \gt 2 \)
The intersection of the two solution sets above is.
\( x \gt 2 \)
Which is the domain of the given function as shown below in the graph of \( f \).

graph of square root function in example 4

Example 5
Find the domain of the function \( f(x) = \sqrt{\dfrac{x + 4}{ {x - 2}}} \).
Solution
The given function takes real values if
\( \dfrac{x + 4}{ {x - 2}} \ge 0\)
We need to solve the above inequality. The zeros of the numerator and denominator are
x = - 4 and x = 2
The zeros split the number line into 3 intervals over which the sign of the inequality is the same. Hence the intervals.
\( (-\infty , -4) \) , \( (-4 , 2 ) \) , \( (2 , \infty) \)
We select a value within each interval and use it to find the sign of the expression \( \dfrac{x + 4}{ {x - 2}}\).
1) On the interval \( (-\infty , -4) \) , select x = -6 and substitute x in \( \dfrac{x + 4}{ {x - 2}} \) by -6 to determine its sign
\( \dfrac{ -6 + 4}{ {-6 - 2}} \gt 0 \)
2) On the interval \( (-4 , 2) \) , select x = 0 and substitute x in \( \dfrac{x + 4}{ {x - 2}} \) by 0 to determine its sign
\( \dfrac{ 0 + 4}{ {0 - 2}} \lt 0 \)
3) On the interval \( (2 , \infty) \) , select x = 3 and substitute x in \( \dfrac{x + 4}{ {x - 2}} \) by 3 to determine its sign
\( \dfrac{ 3 + 4}{ {3 - 2}} \gt 0 \)
Hence the domain is the union of all intervals over which \( \dfrac{x + 4}{ {x - 2}} \gt 0 \) and is given by.
\( (-\infty , -4] \cup (2 , \infty) \)
The graph of \( f \) is as shown below and we may easily check the domain found above. Note x = 2 is not the domain because the division by zero is not allowed.

graph of square root function in example 5

Example 6
Find the domain of the function \( f(x) = \sqrt{-x^2-4} \).
Solution
The given function takes real values if
\( -x^2 - 4 \ge 0\)
The expression \( x^2 + 4 \) is the sum of a square and a positive number. Hence
\( x^2 + 4 \ge 0\)
Multiply all terms of the above inequality by -1 and change the symbol of inequality to obtain
\( - x^2 - 4 \le 0\)
Hence the domain of the given function is an empty set and the given function has no graph. Try to graph it using a graphing calculator.

Example 7
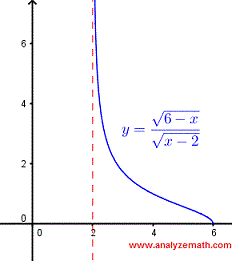
Find the domain of the function \( f(x) = \dfrac{\sqrt{6 - x}}{ \sqrt{x - 2}} \).
Solution
The given function takes real values if two conditions are satisfied.
1) \( 6 - x \ge 0 \) , zero is allowed in the numerator, hence the use of the inequality symbol \( \ge \).
and
2) \( x - 2 \gt 0 \) , zero is not allowed in the denominator, hence the use of the inequality symbol \( \gt \).
The domain of the function is the intersection of the two solution sets of the two inequalities above.
\( x \le 6 \) and \( x \gt 2 \)
The intersection of the two solution sets above is given by the interval.
\( (2 , 6] \)
The graph of \( f \) is as shown below and we may easily check the domain found above. Note x = 2 is not the domain because the division by zero is not allowed.

graph of square root function in example 7

Example 8
Find the domain of the function \( f(x) = \sqrt{x^2 - 4} \).
Solution
The given function takes real values if
\( x^2 - 4 \ge 0\) which can also be written \( (x - 2)(x + 2) \ge 0\)
The solution set to the above quadratic inequality is given by the interval
\( (-\infty , -2] \cup [2 , \infty) \)
The graph of \( f \) is as shown below and we may easily check the domain found above.

graph of square root function in example 8

Example 9
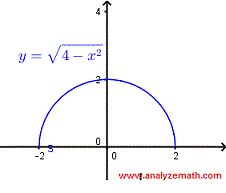
Find the domain of the function \( f(x) = \sqrt{4 - x^2} \).
Solution
The given function takes real values if
\( 4 - x^2 \ge 0\) which can also be written as \( (2 - x)(2 + x) \ge 0\)
The solution set to the above quadratic inequality is given by the interval
\( [2 , 2] \)
The graph of \( f \) is as shown below and we may easily check the domain found above.

graph of square root function in example 9