How to find the domain of rational functions? Examples are presented along with detailed solutions and explanations and also graphical interpretation.
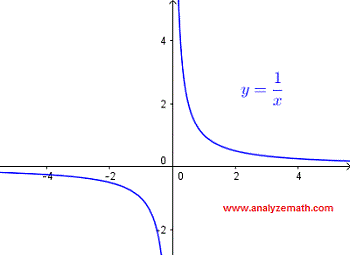
We first need to understand that \( \dfrac{1}{x} \) takes real values only when the denominator is not equal to zero. That is, \( x \ne 0 \).
This restriction can easily be verified by examining the graph of the function \( y = \dfrac{1}{x} \), shown below. The graph "exists" for all values of \( x \) except at \( x = 0 \), where the function is undefined.
The domain of \( \dfrac{1}{x} \), in interval notation, is given by:
\[ (-\infty , 0) \cup (0 , \infty) \]

The given function takes real values and is therefore defined and real for all values of \( x \) except where the denominator is zero.
That occurs when:
\[ x - 2 \ne 0 \quad \Rightarrow \quad x \ne 2 \]In interval notation, the domain of the function is:
\[ (-\infty , 2) \cup (2 , \infty) \]The graph of the function \( f(x) = \dfrac{1}{x - 2} \) is shown below. The function is undefined at \( x = 2 \), which is clearly visible as a vertical asymptote on the graph.

The given function takes real values and is therefore real if:
\[ (x - 1)(x + 2) \ne 0 \]This inequality holds true when \( x \ne 1 \) and \( x \ne -2 \).
In interval notation, the domain of the function is:
\[ (-\infty , -2) \cup (-2 , 1) \cup (1 , \infty) \]Below is the graph of the function \( f(x) = \dfrac{x + 3}{(x - 1)(x + 2)} \), and we can observe that the function is undefined at \( x = -2 \) and \( x = 1 \). At these locations we have vertical asymptotes.

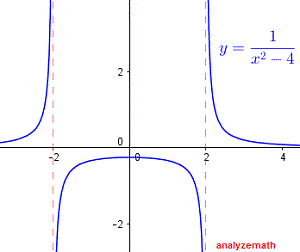
The given function takes real values and is therefore defined and real if the denominator is not equal to zero:
\[ x^2 - 4 \ne 0 \]Factor \( x^2 - 4 \) and rewrite the inequality as:
\[ (x - 2)(x + 2) \ne 0 \]The expression \( (x - 2)(x + 2) \) is not equal to zero if:
\[ x \ne -2 \quad \text{and} \quad x \ne 2 \]In interval notation, the domain of the function is given by:
\[ (-\infty , -2) \cup (-2 , 2) \cup (2 , \infty) \]Below is the graph of the function \( f(x) = \frac{1}{x^2 - 4} \), and we can see that the function is undefined at \( x = -2 \) and \( x = 2 \):
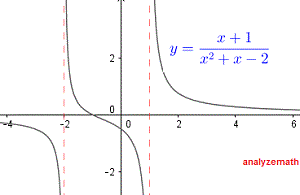
The given function takes real values and is therefore real if:
\[ x^2 + x - 2 \ne 0 \]Factor \( x^2 + x - 2 \) and rewrite the inequality as:
\[ (x - 1)(x + 2) \ne 0 \]The expression \( (x - 1)(x + 2) \) is not equal to zero if \( x \ne 1 \) and \( x \ne -2 \).
In interval form, the domain is given by:
\[ (-\infty, -2) \cup (-2, 1) \cup (1, \infty) \]Below is shown the graph of the function \( f \), and we can see that the given function is undefined at \( x = -2 \) and \( x = 1 \).
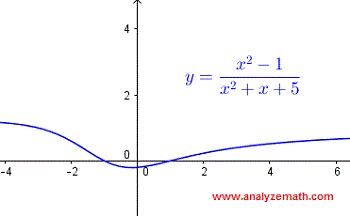
The given function takes real values and is therefore real if:
\[ x^2 + x + 5 \ne 0 \]The expression \( x^2 + x + 5 \) cannot be factored over the reals. We therefore solve the quadratic equation using the discriminant \( \Delta \):
\[ x^2 + x + 5 = 0 \] \[ \Delta = b^2 - 4ac = (1)^2 - 4(1)(5) = -19 \]The discriminant is negative, so there are no real values of \( x \) that make the expression \( x^2 + x + 5 \) equal to zero. Thus, the domain of the function is the set of all real numbers.
In interval notation, the domain is:
\[ (-\infty, \infty) \]Below is the graph of the function \( f(x) = \dfrac{x^2 - 1}{x^2 + x + 5} \), and we can see that it is defined for all real values of \( x \).