3D vectors are introduced along with oprations such the sum, difference and scalar multiplication. Also the properties such as the magnitude are included. Questions with detailed solutions are included.
A vector is a quantity that has both a magnitude and a direction. It is geometrically represented by a line segment whose length is the magnitude and an arrow that indicates its direction as shown in the figure below. Vectors are be used in physics to model quantities with sizes and directions such as velocities, forces, accelerations; in engineering, chemistry, computer graphics, robotics, and many other fields.
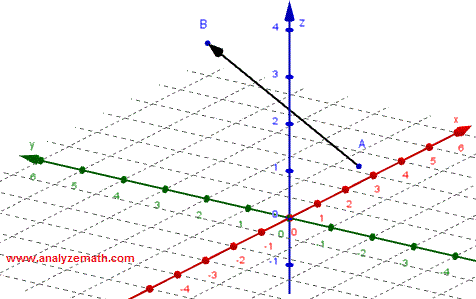
In the above, the vector is defined using an initial point A and a terminal point B. Therefore the vector may be denoted as \( \vec{AB} \).
Vectors with equal magnitudes and same direction are equivalent vectors.
Given two vectors \( \vec{v_1} \) and \( \vec{v_2} \), their sum is a vector obtained by first positioning vector \( \vec{v_2} \) such that its initial point coincide with the terminal point of \( \vec{v_1} \) and the sum \( \vec{v_1} + \vec{v_2} \) is the vector whose initial point is the initial point of \( \vec{v_1} \) and its terminal point is the terminal point of \( \vec{v_2} \). Note that \( \vec{v_1} + \vec{v_2} = \vec{v_2} + \vec{v_1} \). Also the sum of two vectors coincide with the diagonal of the parallelogram determined by \( \vec{v_1} \) and \( \vec{v_2} \).
Given two vectors \( \vec{v_1} \) and \( \vec{v_2} \), the difference \( \vec{v_2} - \vec{v_1} \) may be defined as a sum \( \vec{v_2} + (- \vec{v_1}) \) and represented geometrically as shown below.
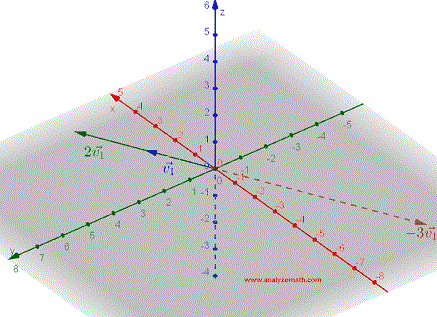
A vector \( \vec{v_1} \) multiplied by a scalar \( k \) is defined as a vector \( k\vec{v_1} \) parallel to \( \vec{v_1} \) and whose direction is the same as that of \( \vec{v_1} \) if k \( k \gt 0 \) 0 and opposite if \( k \lt 0 \). The magnitude (length) of \( k\vec{v_1} \) is \( | k | \) times the magnitude of \( \vec{v_1} \). Figure below shows vectors \( \vec{v_1} \), \( 2\vec{v_1} \) and \( -3 \vec{v_1} \).
A unit vector is a vector with magnitude equal to 1. Below is a shown a 3D rectangular coordinate system with unit vectors \(\vec{i} \), \(\vec{j} \) and \(\vec{k} \) in the positive direction of the x, y and z axes respectively. Vectors \(\vec{i} \), \(\vec{j} \) and \(\vec{k} \) may be defined by their components as follows:
\(\vec{i} = \lt 1 , 0 , 0 >\), one unit along the x axis.
\(\vec{j} = \lt 0,1,0> \), one unit along the y axis.
\(\vec{k} = \lt 0 ,0,1> \) , one unit along the z axis.
The components of any vetor \(\vec{v} \) are defined by expressing \(\vec{v} \) as a sum of multiples of the unit vectors \(\vec{i} \), \(\vec{j} \) and \(\vec{k} \) as follows:
\(\vec{v} = 3\vec{i} + 4\vec{j} + 5\vec{k}\)
or in components form as follows:
\( \vec{v} = \lt 3,4,5> \)
The components of a vector \(\vec{v} \) defined by its initial point \( A = (x_1 , y_1 ,z_1)\) and its terminal point \( B = (x_2 , y_2 ,z_2) \) are given by
\( \vec{v} = \lt x_2-x_1,y_2-y_1,z_2-z_1> \)
Given vector \( \vec{v} = \lt a,b,c> \), its magnitude (or length) is given by
\( ||\vec{v}|| = \sqrt{a^2+b^2+c^2} \).
The unit \( \vec{u} \) vector, defined as a vector of magnitude equal to 1, in the same direction as \( \vec{v} \) is given by
\( u = \dfrac{1}{||\vec{v}||} \vec{v} \)
Given vectors \( \vec{v_1} = \lt a_1,b_1,c_1> \) and \( \vec{v_2} = \lt a_2,b_2,c_2> \), the sum \( \vec{v_1} + \vec{v_2}\) , the difference \( \vec{v_1} - \vec{v_2}\) and scalar multiplication \( k \vec{v_1} \), k a real number, are given by
\( \vec{v_1} + \vec{v_2} = \lt a_1+a_2,b_1+b_2,c_1+c_2> \)
\( \vec{v_1} - \vec{v_2} = \lt a_1 - a_2,b_1 - b_2,c_1 - c_2> \)
\( k \vec{v_1} = \lt k a_1,k b_1,k c_1> \)
Detailed Solutions and explanations to these questions.
More Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
More High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers
More Primary Math (Grades 4 and 5) with Free Questions and Problems With Answers
Home Page
