Algebra Problesm and Questions with Solutions - Grade 12

We rewrite the given expressions to the same power and compare them: \[ 25^{100} \] \[ 2^{300} = (2^3)^{100} = 8^{100} \] \[ 3^{400} = (3^4)^{100} = 81^{100} \] \[ 4^{200} = (4^2)^{100} = 16^{100} \] \[ 2^{600} = (2^6)^{100} = 64^{100} \] Now, we order them from greatest to least: \[ 3^{400} , \quad 2^{600}, \quad 25^{100} , \quad 4^{200} , \quad 2^{300} \]

According to the Rational Root Theorem, the possible rational zeros of a polynomial \[ P(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 \] are given by: \[ \dfrac{\text{factors of the constant term } a_0}{\text{factors of the leading coefficient } a_n}. \]

The leading coefficient is \( 1 \), and its factors are:

\[ \pm 1 \]

The constant term is \( 6 \), and its factors are:

\[ \pm 1, \pm 2, \pm 3, \pm 6 \] - The possible rational zeros are: \[ \pm 1, \pm 2, \pm 3, \pm 6 \]

Testing for Rational Zeros, using direct substitution and calculations:

\[ P(1) = 0, \quad P(2) = 0, \quad P(-3) = 0 \]

Since these values satisfy \( P(x) = 0 \), they are the zeros of \( P(x) \). The polynomial \( P(x) \) has the following rational zeros: \[ x = 1, \quad x = 2, \quad x = -3 \]

Thus, the polynomial can be factored further using these roots.

\[ P(x) = (x-1)(x-2)(x+3) \)

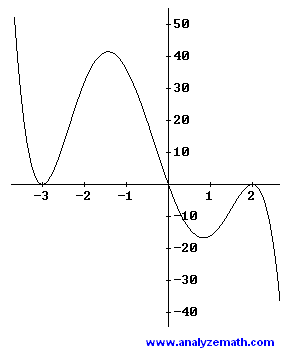From the graph, \(x = -3 \) is a zero of multiplicity \(2\), \(x = 0\) is a zero of multiplicity 1 and \(x = 2\) is a zero of multiplicity 2.

The polynomial has degree 5 and its graph is falling on the right and rising on the left therefore the leading coefficient is negative and equal to \(-1\), hence \( P(x) \) is given by

\[ P(x) = - x (x + 3)^2 (x - 2)^2 \]

Since the coefficients of \( P(x) \) are real, the complex roots must occur in conjugate pairs. Thus, \( 2 + i \) is also a zero of \( P(x) \). Next, we find the quadratic factor corresponding to these two roots: \[ (x - (2 - i))(x - (2 + i)) \] Expanding using the difference of squares: \[ (x - 2 + i)(x - 2 - i) = (x - 2)^2 - i^2 = (x - 2)^2 - (-1) = (x - 2)^2 + 1 \] \[ = x^2 - 4x + 4 + 1 = x^2 - 4x + 5. \] Since \( P(x) \) is divisible by \( x^2 - 4x + 5 \), we perform polynomial division: \[ (x^4 - 4x^3 + 3x^2 + 8x - 10) \div (x^2 - 4x + 5). \] Dividing, we obtain the quotient \( x^2 - 2 \), which factors further as: \[ x^2 - 2 = (x - \sqrt{2})(x + \sqrt{2}). \] Thus, the complete set of zeros of \( P(x) \) is: \[ \mathbf{2 - i, \quad 2 + i, \quad -\sqrt{2}, \quad \sqrt{2}.} \]

We use the vertex form of a quadratic function: \[ f(x) = a (x + 2)^2 + 1 \] where the vertex is given as \( (-2,1) \).

Use the Given Point \( (0, -3) \): Substituting \( x = 0 \) and \( f(0) = -3 \): \[ -3 = a(0 + 2)^2 + 1 \] \[ -3 = 4a + 1 \] Solving for \( a \): \[ 4a = -4 \] \[ a = -1. \] Substituting \( a = -1 \) into the vertex form: \[ f(x) = -(x + 2)^2 + 1 \] Expanding: \[ f(x) = -x^2 - 4x - 3. \] Comparing with the standard quadratic form \( f(x) = ax^2 + bx + c \), we find: \[ a = -1, \quad b = -4, \quad c = -3. \]

\[ f(x) = ax^2 + bx + c \] Given \( f(1) = 3 \), we have: \[ 3 = a + b + c \] Given \( f(5) = 3 \), we have: \[ 3 = 25a + 5b + c \] Subtracting equation B from equation C: \[ (25a + 5b + c) - (a + b + c) = 3 - 3 \] \[ 24a + 4b = 0 \] The x-coordinate of the vertex is given by: \[ \dfrac{-b}{2a} = 3 \] Note that this problem might be solved as follows:

Since \( f(x) \) is a quadratic function such that \( f(1) = 3 \) and \( f(5) = 3 \), the two points \( (1, 3) \) and \( (5, 3) \) lie on the parabola, and since the function is quadratic, the x coordinate of the vertex is equal to x coordinte of the midpoint of these two points since they have the same y coordinte \( 3 \).

The \( x \)-coordinate of the midpoint is: \[ x_{\text{vertex}} = \dfrac{1 + 5}{2} = \dfrac{6}{2} = 3. \] The \( x \)-coordinate of the vertex of the graph of \( f(x) \) is \( \boxed{3} \).

The oblique asymptote is the quotient resulting from the long division of \( a x^4 + b x^3 + 3 \) by \( x^3 - 2 \).

Using long division, we obtain

\[ \dfrac{ax^4 + bx^3 + 3}{x^3 - 2} = ax + b + \dfrac{2ax + (3 + 2b)}{x^3 - 2} \] The quotient \( ax + b \) is the oblique asymptote and it must be equal to \( 2x - 3 \). \[ ax + b = 2x - 3 \] Since two polynomials are equal if and only if their corresponding coefficients are equal, we compare and obtain: \[ a = 2, \quad b = -3 \]

Given \[ \log_9 (x^3) = \log_2(8) \] Simplify right-hand side of the given equation \[ \log_2(8) = \log_2 (2^3) = 3 \] Rewrite the above equation \[ \log_9 (x^3) = 3 \] Rewrite 3 using a logarithm with base 9 \[ \log_9 (x^3) = \log_9(9^3) \] Write the algebraic equation from the previous equation \[ x^3 = 9^3 \] Solve for \(x\) \[ x = 9 \quad \]

Given \[ \log_x(y^3) = 2 \] Rewrite in exponential form \[ x^2 = y^3 \] Square both sides \[ (x^2)^2 = (y^3)^2 \] Simplify \[ x^4 = y^6 \] Take the log of base \(y \) of both sides and simplify \[ \log_y(x^4) = \log_y(y^6) = 6 \]

Given \[ \log_x (8e^3) = 3 \] To solve for \( x \), rewrite the equation in exponential form: \[ x^3 = 8e^3 \] Taking the cube root on both sides: \[ x = \sqrt[3]{8e^3} \] Since \( 8 = 2^3 \), we simplify: \[ x = \sqrt[3]{2^3 e^3} = \sqrt[3]{(2 e)^3} = 2e \]

Given \[ 16^x + 16^{x - 1} = 10 \] Use the exponential rules to write \[ 16^x = (4^2)^x = 4^{2 x} \quad \text{and } 16^{x - 1} = 16^x 16^{-1} = \dfrac{4^{2x}}{16} \] and substitute in the give equation \[ 4^{2x} + \dfrac{4^{2x}}{16} = 10 \] Solve for \( 4^{2x}: \) \[ 4^{2x} = \dfrac{160}{17} \] Take the square root of both sides of the above equation \[ \sqrt {4^{2x}} = \sqrt {(4^x)^2} = 4^x = \dfrac{4\sqrt{10}}{\sqrt{17}} \] Hence \[ 4^x = (2^2)^x = 2^{2x} = \dfrac{4\sqrt{10}}{\sqrt{17}} \] This question could also be solved starting with \[ 16^x = (2^4)^x = 2^{4 x} \] and follow similar steps as in the given solution above.

Given \[ a^2 - b^2 = 8 \] Square both sides and expand \[ a^4 + b^4 - 2a^2b^2 = 8^2 \quad (I) \] Given \[ a b = 2 \] Square both sides of the above \[ (a b)^2 = a^2 b^2 = 2^2 =4 \] Substitute in (I) \[ a^4 + b^4 - 2(4) = 8^2 \] Hence \[ a^4 + b^4 = 72 \]

The range of a sine function is

\[ -1 \leq \sin\left( 2x - \dfrac{\pi}{3} \right) \leq 1 \]

multiply all terms of the double inequality by 2

\[ -2 \leq 2\sin\left( 2x - \dfrac{\pi}{3} \right) \leq 2 \]

Add -5 to all terms of the inequality \[ -2 - 5 \leq 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \leq 2 - 5 \]

Simplify \[ -7 \leq 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \leq -3 \]

Change the above inequality using absolute value \[ 3 \leq \left| 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \right| \leq 7 \]

Add 3 to all terms of the double inequality \[ 3 + 3 \leq \left| 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \right| + 3 \leq 7 + 3 \]

Simplify \[ 6 \leq \left| 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \right| + 3 \leq 10 \] The maximum value of \( f(x) \) is equal to \( 10 \) and the minimum value of \( f(x) \) is equal to \( 6 \).

If \( x \lt -7 \) then \[ x \lt - 3 \]

Add \( 3 \) to the above inequatlity and simplify \[ x + 3 \lt 0 \]

According to the definition of the absolute value \[ |3 + x| = -(3 + x) \]

The given expression simplifies to \[ |4 - |3 + x|| = |4 - (- (3 + x))| = |x + 7| \]

Since \( x + 7 \lt 0 \) \[ |x + 7| = - (x + 7) = - x - 7 \]

and hence \[ |4 - |3 + x|| = -x - 7 \]

Let \( d \) be the distance between \( A \) and \( B \) is \( d \). The time taken to travel from A to B is given by: \[ t_1 = \dfrac{d}{50} \] where \( 50 \) km/hour is the average speed from \( A \) to \( B \).

Let the average speed for the return trip (from \( B \) to \( A \)) be \( v \). The time taken for the return trip is: \[ t_2 = \dfrac{d}{v} \]

The total time for the entire trip is: \[ t_{\text{total}} = t_1 + t_2 = \dfrac{d}{50} + \dfrac{d}{v} \]

The total distance (away and return) is: \[ d + d = 2d \]

The average speed for the whole trip is given by: \[ \text{Average speed} = \dfrac{\text{Total distance}}{\text{Total time}} = \dfrac{2d}{t_{\text{total}}} \] We are told the average speed for the whole trip should be 60 km/hour, so: \[ \dfrac{2d}{\dfrac{d}{50} + \dfrac{d}{v}} = 60 \]

Cancel \( d \) from both the numerator and denominator: \[ \dfrac{2}{\dfrac{1}{50} + \dfrac{1}{v}} = 60 \]

Multiply both sides by \( \left( \dfrac{1}{50} + \dfrac{1}{v} \right) \): \[ 2 = 60 \left( \dfrac{1}{50} + \dfrac{1}{v} \right) \]

Simplify: \[ 2 = \dfrac{60}{50} + \dfrac{60}{v} \] \[ 2 = 1.2 + \dfrac{60}{v} \]

Subtract 1.2 from both sides: \[ 0.8 = \dfrac{60}{v} \]

Solve for \( v \): \[ v = \dfrac{60}{0.8} = 75 \]

Thus, the average speed for the return trip from \( B \) to \( A \) needs to be \( 75 \) km/hour to average \( 60 \) km/hour for the whole trip.

Given \[ x^2 - y^2 = (x - y)(x + y) = -12 \]

Substitute \( x + y \) by 6 in the above \[ 6(x - y) = -12 \]

Solve for \( x - y \) \[ (x - y) = -2 \] We now have a system of equations to solve \[ \begin{cases} x - y = -2 \\ x + y = 6 \end{cases} \]

Solve the system above \[ x = 2, \quad y = 4 \]

Given \[ f(x) + 3f(8 - x) = x \]

Substitute \( x = 2\) in the given equation \[ f(2) + 3 f(6) = 2 \tag{A} \]

Substitute \( x = 6\) in the given equation \[ f(6) + 3 f(2) = 6 \tag{B}\]

Solve equation (B) for \( f(6) \): \[ f(6) = 6 - 3f(2) \tag{C} \]

Substitute into equation (A): \[ f(2) + 3(6 - 3f(2)) = 2 \]

Expand and group \[ - 8 f(2) + 18 = 2 \]

Solve for } f(2): \[ f(2) = 2 \]

Given \[ f(2x + 1) = 2 f(x) + 1 \quad \tag{A} \] let \( x = 1 \) in \( A \) \[ f(3) = 2 f(1) + 1 \quad \tag{B} \] Let \( x = 0 \) in \( A \) \[ f(1) = 2 f(0) + 1 = 2 \times 2 + 1 = 5 \] Substitute \( f(1) = 5 \) in \( B \) to obtain \[ f(3) = 11 \]

Let us find the points of intersections of the circle and the line by solving the system of the two given equations. Substitute \( y \) by \( 2 x + b \) in the eqaution of the circle \[ x^2 + (2 x + b)^2 = 4 \] Expand and simplify \[ 5 x^2 + 4 b x + b^2 - 4 = 0 \] The number of points of intersection is given by the number of solutions of the above equation. The line and circle are tangent if the above quadratic equation has only one solution, which means that the discriminant is equal to zero. Find the discriminant \( \Delta \) as a function of \( b \) \[ \Delta = ( 4 b )^2 - 4 (5)(b^2 - 4)\] Solve. \[ ( 4 b )^2 - 4 (5)(b^2 - 4) = 0 \] \[ -4b^2+80 = 0 \] Solve for \( b \) to obtain two solutions \[ b = \pm 2 \sqrt{5} \]

Let \[ P(x) = x^{100} - x^{99} - x + 1 \quad \text{and} \quad D(x) = x^2 - 3x + 2 \] . The division of the two polynomials may be written as: \[ P(x) = D(x) Q(x) + r(x) \] where \( Q(x) \) is the quotient and \( r(x) \) is the remainder, which will have a degree equal to one or lower because the divisor \( D(x) \) has degree 2. Thus, we express the remainder as \( r(x) = ax + b \).

We now need to find the values of \( a \) and \( b \) that define the remainder.

Note that \( D(x) \) may be factored as follows: \[ D(x) = x^2 - 3x + 2 = (x - 1)(x - 2) \] Hence, we have: \[ P(x) = (x - 1)(x - 2) Q(x) + ax + b \] Using the zeros of \( D(x) \), we write: \[ P(1) = (1 - 1)(1 - 2) Q(1) + a(1) + b \] This simplifies to: \[ a + b = P(1) \] Similarly, we write: \[ P(2) = (2 - 1)(2 - 2) Q(2) + a(2) + b \] This simplifies to: \[ 2a + b = P(2) \] Now we need to evaluate \( P(1) \) and \( P(2) \). \[ P(1) = 1^{100} - 1^{99} - 1 + 1 = 0 \] Next, we rewrite \( P(x) \) as: \[ P(x) = x^{99}(x - 1) - x + 1 \] Hence, we calculate \( P(2) \): \[ P(2) = 2^{99}(2 - 1) - 2 + 1 = 2^{99} - 1 \] We now have a system of equations to solve for \( a \) and \( b \): \[ a + b = 0 \] \[ 2a + b = 2^{99} - 1 \] Solving the system, we get: \[ a = 2^{99} - 1 \quad \text{and} \quad b = 1 - 2^{99} \] Thus, the remainder is: \[ r(x) = (2^{99} - 1)x + 1 - 2^{99} \]

Let \( y = \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \cdots}}} \).

Square both sides to obtain: \[ y^2 = \dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \cdots}}} \] We can write: \[ y^2 = \dfrac{1}{3} + y \] Solve the above quadratic equation to obtain: \[ y = \dfrac{3 + \sqrt{21}}{6} \quad \text{or} \quad y = \dfrac{3 - \sqrt{21}}{6} \] Since \( y \) is positive, the solution is: \[ \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \cdots}}} = y = \dfrac{3 + \sqrt{21}}{6} \]

The coefficient matrix \(A\) is: \[ A = \begin{bmatrix} 2 & 1 & -3 \\ -5 & 3 & 2 \\ 3 & -4 & 1 \end{bmatrix} \] The constants matrix \(b\) is: \[ b = \begin{bmatrix} 5 \\ 7 \\ 8 \end{bmatrix} \]

Cramer's Rule gives the solution for each variable in terms of the determinants of matrices derived from the coefficient matrix \(A\) and modified by replacing columns with the constants from the right-hand side.

To find \(x\), replace the first column of \(A\) with the constants vector \(b\): \[ A_x = \begin{bmatrix} 5 & 1 & -3 \\ 7 & 3 & 2 \\ 8 & -4 & 1 \end{bmatrix} \] Then, the solution for \(x\) is: \[ x = \dfrac{\text{det}(A_x)}{\text{det}(A)} \] To find \(y\), replace the second column of \(A\) with the constants vector \(b\): \[ A_y = \begin{bmatrix} 2 & 5 & -3 \\ -5 & 7 & 2 \\ 3 & 8 & 1 \end{bmatrix} \] Then, the solution for \(y\) is: \[ y = \dfrac{\text{det}(A_y)}{\text{det}(A)} \] To find \(z\), replace the third column of \(A\) with the constants vector \(b\): \[ A_z = \begin{bmatrix} 2 & 1 & 5 \\ -5 & 3 & 7 \\ 3 & -4 & 8 \end{bmatrix} \] Then, the solution for \(z\) is: \[ z = \dfrac{\text{det}(A_z)}{\text{det}(A)} \]

Now, we need to compute the determinants of the matrices \(A\), \(A_x\), \(A_y\), and \(A_z\). \[ \text{det}(A) = \begin{vmatrix} 2 & 1 & -3 \\ -5 & 3 & 2 \\ 3 & -4 & 1 \end{vmatrix} \] Using cofactor expansion along the first row: \[ \text{det}(A) = 2 \begin{vmatrix} 3 & 2 \\ -4 & 1 \end{vmatrix} - 1 \begin{vmatrix} -5 & 2 \\ 3 & 1 \end{vmatrix} + (-3) \begin{vmatrix} -5 & 3 \\ 3 & -4 \end{vmatrix} \] Calculating the 2x2 determinants: \[ \begin{vmatrix} 3 & 2 \\ -4 & 1 \end{vmatrix} = 3(1) - 2(-4) = 3 + 8 = 11 \] \[ \begin{vmatrix} -5 & 2 \\ 3 & 1 \end{vmatrix} = (-5)(1) - (2)(3) = -5 - 6 = -11 \] \[ \begin{vmatrix} -5 & 3 \\ 3 & -4 \end{vmatrix} = (-5)(-4) - (3)(3) = 20 - 9 = 11 \] Substitute these values into the determinant formula: \[ \text{det}(A) = 2(11) - 1(-11) + (-3)(11) = 22 + 11 - 33 = 0 \]

So, \(\text{det}(A) = 0\).

Determinant of \(A_x\): \[ \text{det}(A_x) = \begin{vmatrix} 5 & 1 & -3 \\ 7 & 3 & 2 \\ 8 & -4 & 1 \end{vmatrix} \] We can calculate this using cofactor expansion along the first row: \[ \text{det}(A_x) = 5 \begin{vmatrix} 3 & 2 \\ -4 & 1 \end{vmatrix} - 1 \begin{vmatrix} 7 & 2 \\ 8 & 1 \end{vmatrix} + (-3) \begin{vmatrix} 7 & 3 \\ 8 & -4 \end{vmatrix} \] Calculate the 2x2 determinants: \[ \begin{vmatrix} 3 & 2 \\ -4 & 1 \end{vmatrix} = 11, \quad \begin{vmatrix} 7 & 2 \\ 8 & 1 \end{vmatrix} = -9, \quad \begin{vmatrix} 7 & 3 \\ 8 & -4 \end{vmatrix} = -52 \] Substituting these values into the formula: \[ \text{det}(A_x) = 5(11) - 1(-9) + (-3)(-52) = 55 + 9 + 156 = 220 \] No need to continue: If one of the determnants of \(A_x\), \(A_y\) or \(A_z\) is equal to zero, then the system of equations has no solution.