 .
.
Looking to understand how to solve logarithmic equations? This comprehensive guide provides clear, step-by-step solutions to common types of logarithmic problems. You'll learn to apply key logarithmic rules and properties to solve equations effectively.
\[ \log_b A + \log_b B = \log_b (AB) \] \[ \log_b A - \log_b B = \log_b \left( \dfrac{A}{B} \right) \] \[ \log_b \left( A^n \right) = n \log_b A \] \[ \text{If } \log_b A = \log_b B, \text{ then } A = B \]
Also, the graphical approximation to the solutions of equations of the form \[ f(x) = g(x) \] are shown as the x intercepts of the graph of the function \[ h(x) = f(x) - g(x) \]
Rewrite the equation with the log terms on one side \[ \log(2x - 3) - \log(3 - x) = -2 \]
Rewrite the equation substituting \( -2 \) by \( \log 10^{-2} \) \[ \log(2x - 3) - \log(3 - x) = \log 10^{-2} \]
Use the log rule \( \quad \log A - \log B = \log \left(\dfrac{A}{B}\right) \quad \) to rewrite the equation as follows: \[ \log\left( \dfrac{2x - 3}{3 - x}\right) = \log 10^{-2} \]
Function \( log(x) \) being one-to-one, we can deduce the equation: \[ \dfrac{2x - 3}{3 - x} = 10^{-2} \]
Solve the above equation \[ 2x - 3 = \dfrac{3 - x}{100} \] \[ 200x - 300 = 3 - x \] \[ 201x = 303 \] \[ x = \dfrac{303}{201} = \dfrac{101}{67} \approx 1.51 \]
Check the solution found
Left side: \[ \log\left(2 \cdot \dfrac{101}{67} - 3\right) = \log\left( \dfrac{1}{67}\right) = -\log(67) \]
Right side: \[ \log\left(3 - \dfrac{101}{67}\right) - 2 = \log\left( \dfrac{100}{67}\right) - 2 = \log(100) - \log(67) - 2 = 2 - \log(67) - 2 = -\log(67) \]
The given equation has one solution: \( x = \dfrac{101}{67} \approx 1.51 \)
The x intercept of the graph of the function \( q(x) = \log(2x - 3) - \log(3 - x) + 2 \) (the left side of the given equation written with its right side equal to zero) is shown below. Note that the x intercept is close to the solution obtained analytically above.
 .
.
Use the log rule \(\log A - \log B = \log \left( \dfrac{A}{B}\right)\) to rewrite the left side of the equation as one term and the rule \(n \log(x) = \log(x^n)\) to rewrite the right side as the log of a power. \[ \log \left( \dfrac{x}{x^2 - 1}\right) = \log \left((x - 1)^{-2}\right) \]
Function \(\log(x)\) being a one-to-one function, we can write \[ \dfrac{x}{x^2 - 1} = (x - 1)^{-2} \]
Multiply all terms of the above equation by \((x - 1)^2\) and simplify \[ (x - 1)^2 \cdot \left( \dfrac{x}{x^2 - 1}\right) = (x - 1)^2 \cdot (x - 1)^{-2} \] \[ (x - 1)^2 \cdot \left( \dfrac{x}{x^2 - 1}\right) = 1 \]
Expand \((x - 1)^2\) and \((x^2 - 1)\) and simplify \[ \dfrac{x(x - 1)(x - 1)}{(x + 1)(x - 1)} = 1 \] \[ \dfrac{x(x - 1)}{x + 1} = 1 \]
Multiply both sides of the equation by \(x + 1\) and simplify. \[ x(x - 1) = x + 1 \] \[ x^2 - 2x - 1 = 0 \]
Two solutions: \[ x_1 = 1 + \sqrt{2} \approx 2.41 \quad \text{and} \quad x_2 = 1 - \sqrt{2} \approx -0.41\] Check the solutions found. \[ x_1 = 1 + \sqrt{2} \] Left side of the equation: \(\log(1 + \sqrt{2}) - \log((1 + \sqrt{2})^2 - 1) = \log(1 + \sqrt{2}) - \log(2 + 2\sqrt{2}) = -\log(2)\)
Right side of the equation: \(-2 \log(1 + \sqrt{2} - 1) = -2 \log(\sqrt{2}) = -\log(2)\)
\[ x_2 = 1 - \sqrt{2} \] Left side of the equation: \(\log(1 - \sqrt{2}) - \log((1 - \sqrt{2})^2 - 1)\) is undefined because \(1 - \sqrt{2}\) is negative and the term \(\log(1 - \sqrt{2})\) is undefined.
The given equation has one solution: \( x_1 = 1 + \sqrt{2} \approx 2.41 \)
The \(x\)-intercept of the function \(r(x) = \log x - \log(x^2 - 1) + 2 \log(x - 1)\) is shown below and its \(x\)-coordinate is close to the solution of the equation.
 .
.
Solve the equation: \[ \log_2(2x - 9) = 2 - \log_2(x - 1) \]
Rewrite the equation with terms with log on the same side and substitute \( 2 \) by \( \log_2 4 \) \[ \log_2(2x - 9) + \log_2(x - 1) = \log_2 4 \]
Use the rule \( \log_2 A + \log_2 B = \log_2(AB) \) to rewrite the equation as follows \[ \log_2\left( (2x - 9)(x - 1) \right) = \log_2 4 \] Which gives \[ (2x - 9)(x - 1) = 4 \]
Expand and write in standard form. \[ 2x^2 - 11x + 5 = 0 \]
Solve the above quadratic equation to obtain
Two solutions: \[ x_1 = \dfrac{1}{2} \quad \text{and} \quad x_2 = 5 \]
Check the solutions found. \[ x_1 = \dfrac{1}{2} \]
Left side of the equation: \( \log_2(2 \cdot \dfrac{1}{2} - 9) = \log_2(-8) \) undefined since the argument of the log is negative.
\[ x_2 = 5 \]Left side of the equation: \( \log_2(2 \cdot 5 - 9) = \log_2(1) = 0 \)
Right side of the equation: \( 2 - \log_2(5 - 1) = 2 - \log_2 4 = 0 \)
The given equation has one solution. \( x = 5 \)
The graphical solution is shown below as the x-intercept of the function \( s(x) = \log_2(2x - 9) - 2 + \log_2(x - 1) \).
 .
.
Use the rules \( n \ln x = \ln x^n \) and \( \ln \left( \dfrac{A}{B} \right) = \ln A - \ln B \) to rewrite the equation as follows: \[ \ln(x + 3)^2 - \ln(x + 1) = \ln 2^3 \] \[ \ln \left( \dfrac{(x + 3)^2}{x + 1} \right) = \ln 8 \]
\( \ln x \) is a one-to-one function, hence: \[ \dfrac{(x + 3)^2}{ x + 1} = 8 \quad \text{or} \quad (x + 3)^2 = 8(x + 1) \]
Write the above quadratic equation in standard form: \[ x^2 - 2x + 1 = 0 \] Which gives one solution: \[ x = 1 \]
Check the solutions found:
Left side of the equation: \( 2 \ln(1 + 3) - \ln(1 + 1) = 2 \ln 4 - \ln 2 = 4 \ln 2 - \ln 2 = 3 \ln 2 \)
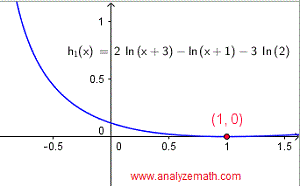
The graphical solution is shown below as the x-intercept of the function:
\[
h_1(x) = 2 \ln(x + 3) - \ln(x + 1) - 3 \ln 2
\]
 .
.
Solve the equation: \[ \left( \log_2(x) \right)^2 - \log_2(x^2) = 8 \]
Use the rules \( n \log_{2} x = \log_{2} x^{n} \) to rewrite the equation as follows: \[ (\log_{2}(x))^{2} - 2 \log_{2}(x) = 8 \]
Let \( u = \log_{2}(x) \) and write the equation in standard form and in terms of \( u \). \[ u^{2} - 2u - 8 = 0 \] Which gives two solutions: \[ u = -2 \quad \text{and} \quad u = 4 \]
We now solve for \( x \): \[ u = -2 = \log_{2}(x) \Rightarrow x = 2^{-2} = \dfrac{1}{4} \] \[ u = 4 = \log_{2}(x) \Rightarrow x = 2^{4} = 16 \]
The graphical solutions are shown below as the \( x \)-intercepts of
\[
p_{1}(x) = (\log_{2}(x))^{2} - \log_{2}(x^{2}) = 8
\]
 .
.
Solve the equation: \[ 10 \log(\log(x)) = 1 \].
Divide both sides by 10 \[ \log(\log(x)) = 0.1 \] Which gives \[ \log(x) = 10^{0.1} \] Which gives \( x \) as \[ x = 10^{10^{0.1}} \approx 18.15 \]
We now solve for \( x \).
The graphical solution is shown below as the \( x \)-intercepts of \( f(x) = 10 \log(\log(x)) - 1 \).
 .
.