Solved Questions on Scalar and Cross Products of 3D Vectors

The cross product \( \vec{u} \times \vec{v} \) is a vector perpendicular to both vectors \( \vec{u} \) and \( \vec{v} \). \[ \text{Hence the dot product of two perpendicular vectors } \vec{u} \text{ and } \vec{u} \times \vec{v} \text{ is equal to } 0. \] \[ \vec{u} \cdot (\vec{u} \times \vec{v}) = 0 \]

If two vectors \( \vec{u} \) and \( \vec{v} \) are perpendicular, then their dot product is equal to 0. Hence: \[ \vec{u} \cdot \vec{v} = \langle -2, -k, 1 \rangle \cdot \langle 8, -2, -3 \rangle = 0 \] Expand the dot product to obtain the equation: \[ (-2)(8) + (-k)(-2) + (1)(-3) = 0 \] Simplify and solve for \( k \): \[ -16 + 2k - 3 = 0 \] \[ k = \dfrac{19}{2} \]

Any two vectors lie on the same plane (i.e., they are coplanar). If a third vector also lies on this plane, then the volume of the parallelepiped formed by the three vectors is zero. This volume is calculated using the scalar triple product: \[ \vec{u} \cdot (\vec{v} \times \vec{w}) = 0 \]

The expression \(\vec{u} \cdot (\vec{v} \times \vec{w})\) is called the scalar triple product and can be computed using the determinant of a 3 by 3 matrix: \[ \vec{u} \cdot (\vec{v} \times \vec{w}) = \det \begin{bmatrix} u_x & u_y & u_z \\ v_x & v_y & v_z \\ w_x & w_y & w_z \end{bmatrix} \] Here, \(u_x, u_y, u_z, v_x, \ldots\) represent the components of the vectors \(\vec{u}, \vec{v}, \vec{w}\).

Substituting the specific vector components into the determinant gives: \[ \vec{u} \cdot (\vec{v} \times \vec{w}) = \det \begin{bmatrix} -3 & 2 & -2 \\ 2 & 1 & k \\ -1 & 3 & -5 \end{bmatrix} \] \[ = -3(-5 - 3k) - 2(-10 + k) - 2(6 + 1) = 21 + 7k \]

For the three vectors to be coplanar, the scalar triple product must equal zero: \[ 21 + 7k = 0 \]

Solving for \(k\): \[ k = -3 \]

Below are the three vectors illustrated lying on the same plane.

Use the definition of the scalar product of two vectors \(\vec{u}\) and \(\vec{v}\) and its expression using the vector components.

Definition: \[ \vec{u} \cdot \vec{v} = \|\vec{u}\| \, \|\vec{v}\| \cos \theta \] where \(\theta\) is the angle between the two vectors. The scalar product is also given by \[ \vec{u} \cdot \vec{v} = u_x v_x + u_y v_y + u_z v_z \] where \(u_x, v_x, u_y, \ldots\) are the components of the vectors \(\vec{u}\) and \(\vec{v}\).

Let us calculate the magnitudes \(\|\vec{u}\|\) and \(\|\vec{v}\|\): \[ \|\vec{u}\| = \sqrt{2^2 + 0^2 + 1^2} = \sqrt{5} \] \[ \|\vec{v}\| = \sqrt{8^2 + (-2)^2 + (-3)^2} = \sqrt{77} \]

We now use the components to find the scalar product: \[ \vec{u} \cdot \vec{v} = (2)(8) + (0)(-2) + (1)(-3) = 13 \]

We now use the definition to find the angle \(\theta\): \[ \vec{u} \cdot \vec{v} = \|\vec{u}\| \, \|\vec{v}\| \cos \theta \] \[ \cos \theta = \dfrac{\vec{u} \cdot \vec{v}}{\|\vec{u}\| \, \|\vec{v}\|} = \dfrac{13}{\sqrt{5} \sqrt{77}} \] \[ \theta = \arccos\left( \dfrac{13}{\sqrt{5} \sqrt{77}} \right) = 48.5^\circ \]

The vector projection of \(\vec{u}\) on \(\vec{v}\) is given by (see formula in Scalar and Cross Products of 3D Vectors): \[ \text{proj}_{\vec{v}}\vec{u} = \dfrac{\vec{u} \cdot \vec{v}}{\|\vec{v}\|^2} \vec{v} \] \[ = \dfrac{ \langle -1,-1,1 \rangle \cdot \langle 2,1,1 \rangle }{2^2 + 1^2 + 1^2} \langle 2,1,1 \rangle = \dfrac{(-1)(2) + (-1)(1) + (1)(1)}{6} \langle 2,1,1 \rangle \] \[ = -\dfrac{2}{6} \langle 2,1,1 \rangle = \langle -2/3, -1/3, -1/3 \rangle \]

Vectors \(\vec{u}\), \(\vec{v}\) and \(\text{proj}_{\vec{v}}\vec{u}\) are shown below.

For triangle ABC to be right at A, the vectors \(\vec{AB}\) and \(\vec{AC}\) have to be perpendicular and therefore their scalar product is equal to 0. We start by calculating the components of the vectors. \[ \vec{AB} = \langle -2, 4, 3 - k \rangle \] \[ \vec{AC} = \langle 2, 1, 6 - k \rangle \] Scalar product of \(\vec{AB}\) and \(\vec{AC}\) has to be zero. \[ \langle -2, 4, 3 - k \rangle \cdot \langle 2, 1, 6 - k \rangle = 0 \] \[ -4 + 4 + (3 - k)(6 - k) = 0 \] Simplify and solve for \(k\). \[ \text{Two solutions: } k = 3 \text{ and } k = 6 \]

Let \( a, b, c \) be the components of vector \( \vec{u} \). Hence \[ \vec{v} \times \vec{u} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 3 & -1 & -2 \\ a & b & c \end{vmatrix} \] \[ = \begin{vmatrix} -1 & -2 \\ b & c \end{vmatrix} \vec{i} - \begin{vmatrix} 3 & -2 \\ a & c \end{vmatrix} \vec{j} + \begin{vmatrix} 3 & -1 \\ a & b \end{vmatrix} \vec{k} = (-c + 2b)\vec{i} + (-2a - 3c)\vec{j} + (3b + a)\vec{k} \]

We now write that the components of \( \vec{v} \times \vec{u} \) and \( \langle 4, 2, 5 \rangle \) are equal as given above. Hence \[ -c + 2b = 4 \] \[ -2a - 3c = 2 \] \[ 3b + a = 5 \]

Note that the equations in the above system are not independent (add -3 times the first equation \( -c + 2b = 4 \) to the second equation \( -2a - 3c = 2 \) and you will obtain an equation equivalent to the third equation \( 3b + a = 5 \)) and therefore it has many solutions. Let \( a = t \) and use the second equation to find \( c \): \[ -2t - 3c = 2 \] \[ c = \dfrac{2 + 2t}{-3} \]

Let \( a = t \) again and use the third equation to find \( b \): \[ 3b + t = 5 \] \[ b = \dfrac{5 - t}{3} \]

We now use the condition \( ||\vec{u}|| = 3 \) to write the equation: \[ \sqrt{a^2 + b^2 + c^2} = 3 \]

Square both sides of the above equation and substitute \( a, b, c \) by their expressions in terms of \( t \): \[ t^2 + \left( \dfrac{5 - t}{3} \right)^2 + \left( \dfrac{2 + 2t}{-3} \right)^2 = 9 \]

Multiply all terms of the equation by 9 and simplify: \[ 9t^2 + (5 - t)^2 + (2 + 2t)^2 = 81 \]

Expand the above to obtain a quadratic equation and solve it to find \[ t = 2 \quad \text{and} \quad t = -\dfrac{13}{7} \]

Hence two solutions for vector \( \vec{u} \): For \( t = 2 \): \[ \vec{u}_1 = \langle t, \dfrac{5 - t}{3}, \dfrac{2 + 2t}{-3} \rangle = \langle 2, 1, -2 \rangle \]

For \( t = -\dfrac{13}{7} \): \[ \vec{u}_2 = \langle t, \dfrac{5 - t}{3}, \dfrac{2 + 2t}{-3} \rangle = \langle -\dfrac{13}{7}, \dfrac{16}{7}, \dfrac{4}{7} \rangle \]

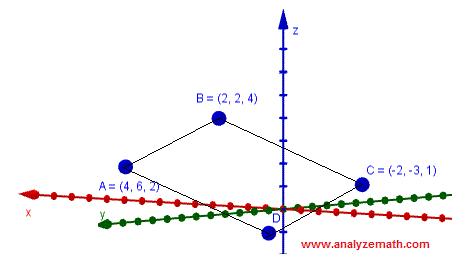
a) Let \( a, b \) and \( c \) be the coordinates of point \( D \), and determine the components of the vectors \( \vec{AB} \) and \( \vec{DC} \). \[ \vec{AB} = \langle 2 - 4 ,\ 2 - 6 ,\ 4 - 2 \rangle = \langle -2, -4, 2 \rangle \] \[ \vec{DC} = \langle -2 - a ,\ -3 - b ,\ 1 - c \rangle \]

For points \( A, B, C \), and \( D \) to form a parallelogram, vectors \( \vec{AB} \) and \( \vec{DC} \) must be equal. Therefore, we have the following vector equation: \[ \langle -2, -4, 2 \rangle = \langle -2 - a, -3 - b, 1 - c \rangle \]

This yields the following three algebraic equations: \[ -2 - a = -2 \] \[ -3 - b = -4 \] \[ 1 - c = 2 \]

Solving these equations gives the coordinates of point \( D \): \[ D(0, 1, -1) \] b) The area \( A \) of the parallelogram is given by: \[ A = \left\| \vec{AB} \times \vec{BC} \right\| \]

First, compute the cross product: \[ \vec{AB} \times \vec{BC} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ -2 & -4 & 2 \\ -4 & -5 & -3 \end{vmatrix} = \begin{vmatrix} -4 & 2 \\ -5 & -3 \end{vmatrix} \vec{i} - \begin{vmatrix} -2 & 2 \\ -4 & -3 \end{vmatrix} \vec{j} + \begin{vmatrix} -2 & -4 \\ -4 & -5 \end{vmatrix} \vec{k} \] \[ = 22\vec{i} + 14\vec{j} -6\vec{k} \]

Now compute the magnitude of this cross product to get the area: \[ A = \left\| \vec{AB} \times \vec{BC} \right\| = \sqrt{22^2 + 14^2 + (-6)^2} = 2\sqrt{179} \]

We first find the components of the vectors \(\vec{AG}\) and \(\vec{BH}\). \[ \vec{AG} = \langle 2, 2, 2 \rangle \] \[ \vec{BH} = \langle -2, 2, 2 \rangle \]

Using the dot product, with \(\theta\) being the angle between the vectors \(\vec{AG}\) and \(\vec{BH}\), we have (see question 5 above): \[ \cos \theta = \dfrac{\vec{AG} \cdot \vec{BH}}{||\vec{AG}|| \cdot || \vec{BH} ||} = \dfrac{2\cdot (-2)+2\cdot2+2\cdot2}{\sqrt{2^2+2^2+2^2}\sqrt{(-2)^2+2^2+2^2}} = \dfrac{1}{3} \] \[ \theta = \arccos \left( \dfrac{1}{3} \right) \approx 70.5^{\circ} \]

To find a vector orthogonal to the plane containing points \( A(1,2,-3) \), \( B(0,-2,1) \), and \( C(-2,0,1) \), we first compute two vectors in the plane: \[ \vec{AB} = \langle 0 - 1,\ -2 - 2,\ 1 - (-3) \rangle = \langle -1, -4, 4 \rangle \] \[ \vec{AC} = \langle -2 - 1,\ 0 - 2,\ 1 - (-3) \rangle = \langle -3, -2, 4 \rangle \] Next, compute the cross product \( \vec{AB} \times \vec{AC} \) to find a vector orthogonal to both (and thus normal to the plane): \[ \vec{AB} \times \vec{AC} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ -1 & -4 & 4 \\ -3 & -2 & 4 \end{vmatrix} = \left( (-4)(4) - (4)(-2) \right)\vec{i} - \left( (-1)(4) - (4)(-3) \right)\vec{j} + \left( (-1)(-2) - (-4)(-3) \right)\vec{k} \] \[ = (-16 + 8)\vec{i} - (-4 + 12)\vec{j} + (2 - 12)\vec{k} = \langle -8, -8, -10 \rangle \] Thus, a vector orthogonal to the plane is: \[ {\langle -8, -8, -10 \rangle} \]

The area \( A \) of a triangle is given by half the magnitude of the cross product \( A_t \) of any two vectors made by the sides of the triangle. Hence
\( A_t = \vec{AB} \times \vec{AC} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ 0 & -2 & 3 \\ -1 & 2 & 4 \end{vmatrix}} = {\begin{vmatrix} -2 & 3 \\ 2 & 4 \end{vmatrix}} \vec{i} - {\begin{vmatrix}0 & 3\\ -1 & 4\end{vmatrix}} \vec{j} + {\begin{vmatrix}0 & -2\\ -1& 2\end{vmatrix}} \vec{k} = -14\vec{i} - 3\vec{j} -2\vec{k} \)
\( A_t = (1/2) || \vec{AB} \times \vec{AC} || = \sqrt{(-14)^2 + (-3)^2 + (-2)^2} = (1/2) \sqrt{209} \) unit²

The volume \( V \) of the parallelepiped is given by \[ V = |\vec{u} \cdot (\vec{v} \times \vec{w})| = |\vec{v} \cdot (\vec{w} \times \vec{u})| = |\vec{w} \cdot (\vec{v} \times \vec{u})| \] Let us first find the components of the vectors \( \vec{u} \), \( \vec{v} \), and \( \vec{w} \). \[ \vec{u} = \langle -3, 0, 7 \rangle \] \[ \vec{v} = \langle -8, 0, 0 \rangle \] \[ \vec{w} = \langle 0, -9, 0 \rangle \] \[ \vec{u} \cdot (\vec{v} \times \vec{w}) = \langle -3 , 0 , 7 \rangle \cdot \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ -8 & 0 & 0 \\ 0 & -9 & 0 \end{vmatrix} \] \[ = \langle -3 , 0 , 7 \rangle \cdot \left\{ \begin{vmatrix} 0 & 0 \\ -9 & 0 \end{vmatrix} \vec{i} - \begin{vmatrix} -8 & 0 \\ 0 & 0 \end{vmatrix} \vec{j} + \begin{vmatrix} -8 & 0 \\ 0 & -9 \end{vmatrix} \vec{k} \right\} \] \[ = \langle -3 , 0 , 7 \rangle \cdot \langle 0 , 0 , 72 \rangle = 0 + 0 + 7 \cdot 72 = 504 \] The volume is \[ V = |504| = 504 \quad \text{unit}^3 \]